Fundamental Theorem of Calculus is the basic theorem that is widely used for defining a relation between integrating a function with that of differentiating a function. The fundamental theorem of calculus is widely useful for solving various differential and integral problems and making the solution easy for students.
This is widely used in the fields of physics, engineering, medicine, economics, biology, space exploration, statistics, pharmacology, and many more.
Before learning about the fundamental theorem of calculus let’s first learn about calculus and others. In this article, we will learn about calculus, area function, the fundamental theorem of calculus, and others in this article.
What is Calculus?
Calculus is the most important branch of Mathematics and it is the backbone of modern society it is widely used in every aspect of our life. The history of calculus dates back to ancient Egypt. Historians say that the method used by Egyptians to calculate the volume of a pyramidal frustum was integral calculus. They knew about the basic functions of integral calculus and used them to calculate volumes and area. However, modern calculus was developed by Isaac Newton and Gottfried Wilhelm Leibniz independently.
There are two branches of calculus,
- Differential Calculus
- Integral Calculus
Differential Calculus
In this branch of calculus, we divide things into different pieces and study how they change from one moment to the next. For example, change in velocity with respect to time.
Integral Calculus
In this branch of calculus, we join the small pieces together to understand their overall behaviour. For example, in determining the length of power cable required to connect the two substations.
Area Function
Let us consider a function f(t) continuous in the interval [a, b], as shown in the below image:
Now, let’s mark some point x between a and b on the graph.
Now, we must find the area under the curve y = f(t) between the interval [a, x].
So, the area under the curve between a and x is the definite integral from a to x of f(t) dt, is
A(x) = ∫ax f(t) dt
Here A(x) is known as the area function and it is helpful in finding the fundamental theorem of calculus. Or in other words, A(x), i.e., ∫ax f(t) dt is the area of the region bounded by the curve y = f(t) on the x-axis with coordinates a and b. If x is a point in between [a, b] interval then ∫ax f(t) dt will represent the area of the shaded region, which is A(x).
Example:
Let’s find out the value of A(x) for function y = 2x between x = 2 and x = 6.
A(x) = ∫26 2x dx
= [x2]26
= 62 – 22
= 36 – 4
= 32 square units
Learn more about Area Under The Curve
Fundamental Theorem of Calculus
The fundamental theorem of calculus is a powerful theorem in mathematics. It set up a relationship between differentiation and integration. Now, this relationship gives us a method to evaluate definite internal without calculating areas or using Riemann sums. The fundamental theorem is divided into two parts:
- First fundamental theorem
- Second fundamental theorem
Now we will discuss each theorem one by one in detail:
First Fundamental Theorem of Calculus (Part 1)
The First Fundamental Theorem of Calculus also called “Fundamental Theorem Part 1” states that if f(x) is a continuous function on the closed interval [a, b] and the function F(x) is defined by
F(x) = ∫ax f(t) dt
Then,
F'(x) = f(x) over [a, b]
where, F'(x) is derivative of F(x)
Proof for First Fundamental Theorem of Calculus
The proof of the first fundamental theorem of calculus is explained below:
According to the fundamental theorem of calculus, we have
For, F(x) = ∫ax f(t) dt
F'(x) = f(x) …(A)
Now, equation (A) can be written as
F'(x) = lim h⇢0 [F(x + h) – F(x]/h
= lim h⇢0 1/h [( ∫ax+h f(t) dt – ∫ax f(t) dt )] …(B)
Thus, equation (B) represents the area under the curve y = f(t) on the interval [x, x + h]. Now, equation (B) can be written as
F'(x) = lim h⇢0 1/h (∫xx+h f(t) dt …(C)
Now, according to the mean value theorem of the definite integral,
If there exists a c such that x ≤ c ≤ x + h then,
f(c) = 1/h ∫xx+h f(t) dt
Thus,
F'(x) = lim h⇢0 f(c)
Since c is in between x and x + h, therefore c⇢x as h⇢0.
Also, since f(x) is continuous, therefore we have,
lim h⇢0 f(c) = lim c⇢x f(c) = f(x)
Thus,
F'(x) = lim h⇢0 1/h ∫xx+h f(t) dt
= lim h⇢0 f(c)
= f(x)
Hence, proved.
Note
- Every continuous function f has an antiderivative F(x).
- The fundamental theorem of calculus connects integral calculus and differential calculus.
Finding Derivative using Fundamental Theorem of Calculus
We can easily calculate the derivative of any function with the help of the Fundamental Theorem of Calculus. Let us discuss this concept with the help of an example,
Example: Evaluate F'(4) if F(x) = ∫4x √(t3) dt.
Solution:
According to Fundamental Theorem of Calculus
F'(x) = √(x3)
Thus, F'(4) = √(43) = 43/2 = (41/2)3 = (√4)3 = 23 = 8.
Thus, the question is solved using the fundamental theorem of calculus.
Second Fundamental Theorem of Calculus (Part 2)
Second Fundamental Theorem of calculus also called the Fundamental Theorem of Calculus Part 2 states that, if f(x) is continuous on the closed interval [a, b] and F(x) is the antiderivative of f(x), then
∫ab f(x) dx = F(b) – F(a)
The second fundamental theorem is also known as the evaluation theorem. This theorem says that the solution of ∫ab f(x) dx is equal to the difference between the value of the F at the upper limit b and the value of F at the lower limit a.
Remark on Second Fundamental Theorem of Calculus
Various remarks for Second Fundamental Theorem are,
- In ∫ab f(x) dx expression, the function f(x) must be well defined and continuous in [a, b] interval.
- It is a very helpful theorem as it provides a method of estimating the definite integral without finding the sum’s limit.
- In estimating the definite integral, the main operation is finding a function whose derivative is the equation to integrate and this process will strengthen the differentiation and integration relationship.
Proof for Second Fundamental Theorem of Calculus
The proof of the Second Fundamental Theorem of Calculus is mentioned below:
Let’s take any continuous function ‘f’ such that
F(x) = ∫cx f(t) dt
where c is the arbitrary constant thus if we show that, F'(x) = f(x) it implies that ∫ab f(x) dx = F(b) – F(a)
Using the definition of Limit,
F'(x) = lim h–>0 [F(x+h) – F(x)]/h
= lim h–>0 [∫cx+h f(t) dt – ∫cx f(t) dt]/h
using the property of definite integrals.
= lim h–>0 [∫xx+h f(t) dt]/h
We know that for very small values of h
∫xx+h f(t) dt = f(x).h
F'(x) = lim h–>0 [ f(x).h]/h
F'(x) = lim h–>0 f(x)
F'(x) = f(x)
Thus, the Second Fundamental Theorem of Calculus is verified.
Read More,
Solved Examples on Fundamental Theorem of Calculus
Example 1. Calculate the derivative of the function 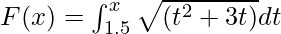 at x = 3.
at x = 3.
Solution:
Given that 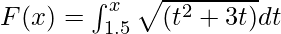
So, using first FTC, we get
F'(x) = 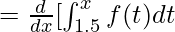 = √(x2 + 3x)
= √(x2 + 3x)
Therefore,
F'(3) = √(32 + 3.3) = √(9 + 9) = √(2.9) = 3√2.
Example 2. Calculate the derivative of the function 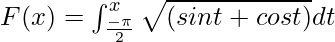 at x = π/2.
at x = π/2.
Solution:
Given that 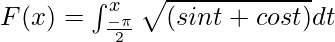
So, using first FTC, we get
F'(x) =  = f(x)
= f(x)
Hence,
F'(x) = √(sin x + cos x)
Therefore,
F'(π/2) = √(sin π/2 + cos π/2) = √(1 + 0) = 1.
Example 3. Find the derivative of 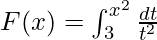 .
.
Solution:
Given that 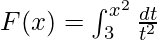
So, let x2 = u.
Now, consider a new function,
G(u) = ∫3u dt/t2
G'(u) = 1/u2
Since, F(x) = G(x2)
F'(x) = G'(x2).2x
F'(x) = (1/x4).2x
F'(x) = 2/x3.
Example 4. Find the derivative of the 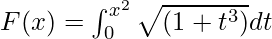 .
.
Solution:
Given that 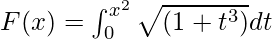
So, let x2 = u.
Now, consider a new function,
G(u) = ∫0u √(1 + t3) dt
Using first FTC, we have
G'(u) = √(1 + u3)
As F(x) = G(x2)
F'(x) = G'(x2).2x
F'(x) = 2x √(1 + (x2)3)
F'(x) = 2x √(1 + x6).
Example 5. Find the derivative of the function 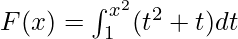 .
.
Solution:
Given that 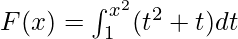
So, let x2 = u.
Now, considering new function,
G(u) = ∫1u (t2 + t) dt.
Using first FTC, we get
G'(u) = u2 + u
Since, F(x) = G(x2)
F'(x) = G'(x2).2x
F'(x) = (x4 + x).2x
F'(x) = 2x5 + 2x2.
Example 6. Evaluate the integral  .
.
Solution:
Given that 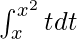
Now we find the anti-derivative of t
∫t dt = t2 + C
Now using the second FTC, we get
∫ab f(x) dx = F(b) – F(a)
 = F(x2) – F(x)
= F(x2) – F(x)
 = ((t2)2) – (t2)
= ((t2)2) – (t2)
 = (t4) – (t2)
= (t4) – (t2)
 = t2((t2) – 1)
= t2((t2) – 1)
Example 7. Evaluate the integral 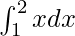 .
.
Solution:
Given that I = 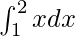
Now using the second FTC, we get
∫ab f(x) dx = F(b) – F(a)
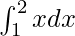 = F(2) – F(1)
= F(2) – F(1)
Now we find the anti-derivative of x
∫x dx = x2 + C
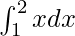 = (22) – 1
= (22) – 1
= 4 – 1
= 3
Example 8: Evaluate the integral ∫02 (x2 – x) dx.
Solution:
Given I = ∫02 (x2 – x) dx
Using second FTC, we get
∫ab f(x) dx = F(b) – F(a)
∫02 (x2 – x) dx = F(2) – F(0)
Now we find the anti-derivative of x
∫02 (x2 – x) dx = x3/3 – x2/2
So,
= [x3/3 – x2/2]02
= [8/3 – 4/2]
= [8/3 – 2]
= [8/3 – 6/3]
= 2/3.
Example 9: Evaluate the integral F(x) = ∫0x et + e-t dt.
Solution:
Given that F(x) = ∫0x et + e-t dt
Using the first FTC, we get
F'(x) = ex + e-x.
Example 10: Find the integral of 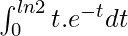 .
.
Solution:
Given I = 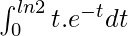
so we can also write as
I = 
Now apply integration by parts, we get
u = t, dv = d(e-t)
So, du = 1, v = e-t
So, the integral is
I = –
=![Rendered by QuickLaTeX.com [(te^{-t})|^{ln2}_0 - \int_0^{ln2} e^{-t} dt]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cdb9c047410f042e043a963cf24c9630_l3.png)
= ![Rendered by QuickLaTeX.com [(te^{-t})|^{ln2}_0 + \int_0^{ln2} e^{-t} dt]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-93754af9b1562facb9a10f4571e94ee8_l3.png)
=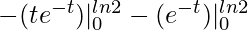
= ![Rendered by QuickLaTeX.com - [e^{-t}(t + 1)]|^{ln2}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ece2e1920a79b5bb6427530afc452dfa_l3.png)
= -e-ln2(ln2 + 1) + e0 .1
= 1/2(ln e – ln 2)
= 1/2 ln e/2
FAQs on Fundamental Theorem of Calculus
Q1: What is the Fundamental Theorem of Calculus?
Answer:
The fundamental theorem of calculus is a basic theorem which provides a relation between the differentiation of the function and the integration of the function.
Q2: How many Fundamental Theorems of Calculus are there?
Answer:
There are two basic Fundamental Theorem of Calculus that are,
- First Fundamental Theorem of Calculus
- Second Fundamental Theorem of Calculus
Q3: What is First Fundamental Theorem of Calculus?
Answer:
The first fundamental theorem of calculus states that “For any continuous function f defined on the closed interval [a, b] and A (x) be the area function.
Then A′(x) = f (x), for every x ∈ [a, b].
Q4: What is Second Fundamental Theorem of Calculus?
Answer:
The second fundamental theorem of integral states that “For any continuous function f defined on the closed interval [a, b] and F be the antiderivative of f.
Then ∫ab f(x) dx = F(b) – F(a)
Q5: Who proved Fundamental Theorem of Calculus?
Answer:
The credit for proving the fundamental theorem of calculus is given to James Gregory and this was further finalised by Issac Newton.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...