Full domain Hashing with variable Hash size in Python
Last Updated :
11 Jun, 2021
A cryptographic hash function is a special class of hash function that has certain properties which make it suitable for use in cryptography. It is a mathematical algorithm that maps data of arbitrary size to a bit string of a fixed size (a hash function) which is designed to also be a one-way function, that is, a function which is infeasible to invert. In this article, let us understand one such type of hashing with variable hash size.
Traditional RSA Signature schemes are based on the following sequence of steps:
- Obtain the message to be digitally signed – M
- Use SHA or some other hashing algorithm to generate the message digest – H = Hash(M)
- Encrypt the message digest using the signer’s private key. The encryption results is the signature of the message – S = E(PrivateKey, H)
One potential deficit in the above-illustrated scheme is that the RSA system ends up being underutilized. Let us assume that the RSA modulus is of the order of 2048 bits. This means that the input can be any value with up to 2048 bits. However, in the signature scheme, the input to the RSA system is consistently the same size, the size of the hash-digest. Therefore, if, for instance, SHA-512 is being utilized in the signature scheme, all inputs to the RSA function will consistently be 512 bits. This leaves the majority (> 99% in this case) of the RSA input space unutilized. This has the effect of reducing the overall security level of the RSA system as a result of the input space underutilization.

The Full Domain Hashing (FDH) scheme in RSA Signature schemes mitigates this underutilization by hashing the message onto the full domain of the RSA cryptosystem. The goal of FDH, therefore, is:
Hash a message using a function whose image-size/digest-size equals the size of the RSA modulus
The two basic approaches to realize a function which can produce an arbitrary size digest are:
- Repeatedly hashing the message (with slight modifications) and concatenating
- Using an eXtendible Output Function (XOF) hashing methods
Repeated Hashing with Concatenation
Although traditional hashing algorithms such as SHA1, SHA256, SHA512 do not nearly have the sufficient range to cover the input domains of RSA systems, we can construct a full domain hashing method through the repeated application of these hash functions. The standard hash function, say SHA512, is applied to the message repeatedly, concatenating the results each time. This is done until the requisite number of bits is achieved.
To introduce the randomized behaviour of hash functions, instead of hashing the same message repeatedly, some modifications are introduced to the message at each iteration before performing the hashing. An example of such a modification would be to concatenate the iteration count to the message, before hashing. Thus, an FDH function is realized as:
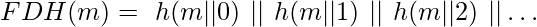
If the SHA512 hash was computed and concatenated N times, the overall hash will have a bit size of N * 512. Assuming that this value is greater than the required number, ‘K’, of bits, we can extract the leading K bits to obtain the desired length hash.
Below is the implementation of the above approach:
Python3
import binascii
from math import ceil
from hashlib import sha256
def fdh(message, n):
result = []
for i in range(ceil(n / 256)):
currentMsg = str(message) + str(i)
result.append(sha256((currentMsg).encode()).hexdigest())
result = ''.join(result)
resAsBinary = ''.join(format(ord(x), 'b') for x in result)
resAsBinary = resAsBinary[:n]
return binascii.unhexlify('00%x' % int(resAsBinary, 2)).hex()
if __name__ == '__main__':
message = "GeeksForGeeks"
print(fdh(message, 600))
|
Output:
00cf161c36df4db9e30d79cf9cb3d72e1934cbaeb9eb8638f0d71f1872679e1df9c3932c77c70c98efa64d34e3166c5b698738b36d9b36b87261c5ae3c61873c98e19b362db1c73658f0e4c9
Using an eXtendible Output Function (XOF) hashing methods
eXtendible Output Functions are a class of hashing functions which, unlike traditional hashing functions, can generate an arbitrarily large sequence of bits in the digest of a message. This is in strong contrast to regular hash functions which are defined by a fixed output size. In the recently introduced SHA-3 scheme, XOF is provided using the SHAKE128 and SHAKE256 algorithms. They follow from the general properties of the sponge construction. A sponge function can generate an arbitrary length of the output. The 128 and 256 in their names indicate its maximum security level (in bits), as described in Sections A.1 and A.2 of FIPS 202.
To avail the functionality of SHA-3 in Python, the PyCryptodome library may be utilized as follows:
Python3
from Crypto.Hash import SHAKE256
from binascii import hexlify
shake = SHAKE256.new()
shake.update(b'GeeksForGeeks')
print(hexlify(shake.read(50)))
|
Output:
b’65d6df8d88198de69b3cf59b859d72971b93f102ca20af812b931714a558c7a134cb3bb085835f470c890bd1d50928355358′
Note: The above code won’t be run on online IDE’s because online IDE’s lack the Crypto library.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...