Friends Pairing Problem

Given n friends, each one can remain single or can be paired up with some other friend. Each friend can be paired only once. Find out the total number of ways in which friends can remain single or can be paired up. 

Examples:

Input  : n = 3
Output : 4
Explanation:
{1}, {2}, {3} : all single
{1}, {2, 3} : 2 and 3 paired but 1 is single.
{1, 2}, {3} : 1 and 2 are paired but 3 is single.
{1, 3}, {2} : 1 and 3 are paired but 2 is single.
Note that {1, 2} and {2, 1} are considered same.

Mathematical Explanation:
The problem is simplified version of how many ways we can divide n elements into multiple groups.
(here group size will be max of 2 elements).
In case of n = 3, we have only 2 ways to make a group: 
    1) all elements are individual(1,1,1)
    2) a pair and individual (2,1)
In case of n = 4, we have 3 ways to form a group:
    1) all elements are individual (1,1,1,1)
    2) 2 individuals and one pair (2,1,1)
    3) 2 separate pairs (2,2)

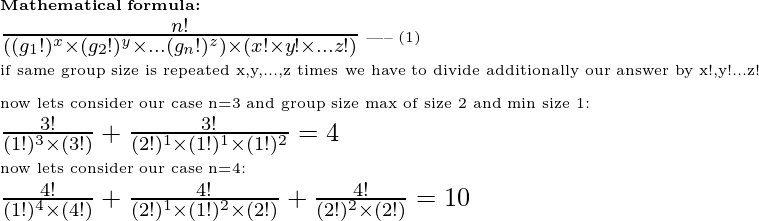
For n-th person there are two choices:1) n-th person remains single, we recur for f(n – 1)2) n-th person pairs up with any of the remaining n – 1 persons. We get (n – 1) * f(n – 2)Therefore we can recursively write f(n) as:f(n) = f(n – 1) + (n – 1) * f(n – 2)

Since the above recursive formula has overlapping subproblems, we can solve it using Dynamic Programming.  

C++

// C++ program for solution of
// friends pairing problem
#include <bits/stdc++.h>
using namespace std;

// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(int n)
{
    int dp[n + 1];

    // Filling dp[] in bottom-up manner using
    // recursive formula explained above.
    for (int i = 0; i <= n; i++) {
        if (i <= 2)
            dp[i] = i;
        else
            dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
    }

    return dp[n];
}

// Driver code
int main()
{
    int n = 4;
    cout << countFriendsPairings(n) << endl;
    return 0;
}

Java

// Java program for solution of
// friends pairing problem
import java.io.*;

class GFG {

    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int dp[] = new int[n + 1];

        // Filling dp[] in bottom-up manner using
        // recursive formula explained above.
        for (int i = 0; i <= n; i++) {
            if (i <= 2)
                dp[i] = i;
            else
                dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
        }

        return dp[n];
    }

    // Driver code
    public static void main(String[] args)
    {
        int n = 4;
        System.out.println(countFriendsPairings(n));
    }
}

// This code is contributed by vt_m

Python3

# Python program solution of
# friends pairing problem

# Returns count of ways
# n people can remain
# single or paired up.
def countFriendsPairings(n):

    dp = [0 for i in range(n + 1)]

    # Filling dp[] in bottom-up manner using
    # recursive formula explained above.
    for i in range(n + 1):

        if(i <= 2):
            dp[i] = i
        else:
            dp[i] = dp[i - 1] + (i - 1) * dp[i - 2]

    return dp[n]

# Driver code
n = 4
print(countFriendsPairings(n))

# This code is contributed
# by Soumen Ghosh.

C#

// C# program solution for
// friends pairing problem
using System;

class GFG {

    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int[] dp = new int[n + 1];

        // Filling dp[] in bottom-up manner using
        // recursive formula explained above.
        for (int i = 0; i <= n; i++) {
            if (i <= 2)
                dp[i] = i;
            else
                dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
        }

        return dp[n];
    }

    // Driver code
    public static void Main()
    {
        int n = 4;
        Console.Write(countFriendsPairings(n));
    }
}

// This code is contributed by nitin mittal.

PHP

<?php
// PHP program solution for
// friends pairing problem

// Returns count of ways n people
// can remain single or paired up.
function countFriendsPairings($n)
{
    $dp[$n + 1] = 0;

    // Filling dp[] in bottom-up
    // manner using recursive formula
    // explained above.
    for ($i = 0; $i <= $n; $i++)
    {
        if ($i <= 2)
        $dp[$i] = $i;
        else
        $dp[$i] = $dp[$i - 1] +
                     ($i - 1) *
                   $dp[$i - 2];
    }

    return $dp[$n];
}

// Driver code
$n = 4;
echo countFriendsPairings($n) ;

// This code is contributed
// by nitin mittal.
?>

Javascript

<script>

// Javascript program for solution of
// friends pairing problem


// Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings(n)
    {
        let dp = [];

        // Filling dp[] in bottom-up manner using
        // recursive formula explained above.
        for (let i = 0; i <= n; i++) {
            if (i <= 2)
                dp[i] = i;
            else
                dp[i] = dp[i - 1] + (i - 1) * dp[i - 2];
        }

        return dp[n];
    }


// Driver Code

        let n = 4;
        document.write(countFriendsPairings(n));

</script>

Output

10

Time Complexity : O(n) 
Auxiliary Space : O(n)

Another approach: (Using recursion)  

C++

// C++ program for solution of friends
// pairing problem Using Recursion
#include <bits/stdc++.h>
using namespace std;

int dp[1000];

// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(int n)
{
    if (dp[n] != -1)
        return dp[n];

    if (n > 2)
        return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
    else
        return dp[n] = n;
}

// Driver code
int main()
{
    memset(dp, -1, sizeof(dp));
    int n = 4;
    cout << countFriendsPairings(n) << endl;
    // this code is contributed by Kushdeep Mittal
}

Java

// Java program for solution of friends
// pairing problem Using Recursion
import java.io.*;
class GFG {
    static int[] dp = new int[1000];

    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        if (dp[n] != -1)
            return dp[n];

        if (n > 2)
            return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
        else
            return dp[n] = n;
    }

    // Driver code
    public static void main(String[] args)
    {
        for (int i = 0; i < 1000; i++)
            dp[i] = -1;
        int n = 4;
        System.out.println(countFriendsPairings(n));
    }
}

// This code is contributed by Ita_c.

Python3

# Python3 program for solution of friends
# pairing problem Using Recursion
dp = [-1] * 1000
# Returns count of ways n people
# can remain single or paired up.
def countFriendsPairings(n):
    global dp

    if(dp[n] != -1):
        return dp[n]

    if(n > 2):

        dp[n] = (countFriendsPairings(n - 1) +
                (n - 1) * countFriendsPairings(n - 2))
        return dp[n]

    else:
        dp[n] = n
        return dp[n]

# Driver Code
n = 4
print(countFriendsPairings(n))

# This code contributed by PrinciRaj1992

C#

// C# program for solution of friends
// pairing problem Using Recursion
using System;

class GFG {
    static int[] dp = new int[1000];

    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        if (dp[n] != -1)
            return dp[n];

        if (n > 2)
            return dp[n] = countFriendsPairings(n - 1) + (n - 1) * countFriendsPairings(n - 2);
        else
            return dp[n] = n;
    }

    // Driver code
    static void Main()
    {
        for (int i = 0; i < 1000; i++)
            dp[i] = -1;
        int n = 4;
        Console.Write(countFriendsPairings(n));
    }
}

// This code is contributed by DrRoot_

PHP

<?php
// PHP program for solution of friends
// pairing problem Using Recursion

// Returns count of ways n people
// can remain single or paired up.
function countFriendsPairings($n)
{
    $dp = array_fill(0, 1000, -1);

    if($dp[$n] != -1)
    return $dp[$n];

    if($n > 2)
    {
        $dp[$n] = countFriendsPairings($n - 1) + ($n - 1) *
                  countFriendsPairings($n - 2);
        return $dp[$n];
    }
    else
    {
        $dp[$n] = $n;
        return $dp[$n];
    }
}

// Driver Code
$n = 4;
echo countFriendsPairings($n)

// This code is contributed by Ryuga
?>

Javascript

<script>

// Javascript program for solution of friends
// pairing problem Using Recursion

    let dp = new Array(1000);

    // Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings(n)
    {
        if (dp[n] != -1)
            return dp[n];

        if (n > 2)
            return dp[n] = countFriendsPairings(n - 1)
            + (n - 1) * countFriendsPairings(n - 2);
        else
            return dp[n] = n;
    }

    // Driver code
    for (let i = 0; i < 1000; i++)
        dp[i] = -1;
    let n = 4;
    document.write(countFriendsPairings(n));

    // This code is contributed by rag2127

</script>

Output

10

Time Complexity : O(n) 
Auxiliary Space : O(n)

Since the above formula is similar to fibonacci number, we can optimize the space with an iterative solution.  

C++

#include <bits/stdc++.h>
using namespace std;

// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(int n)
{
    int a = 1, b = 2, c = 0;
    if (n <= 2) {
        return n;
    }
    for (int i = 3; i <= n; i++) {
        c = b + (i - 1) * a;
        a = b;
        b = c;
    }
    return c;
}

// Driver code
int main()
{
    int n = 4;
    cout << countFriendsPairings(n);
    return 0;
}

// This code is contributed by mits

Java

import java.io.*;
class GFG {
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int a = 1, b = 2, c = 0;
        if (n <= 2) {
            return n;
        }
        for (int i = 3; i <= n; i++) {
            c = b + (i - 1) * a;
            a = b;
            b = c;
        }
        return c;
    }

    // Driver code
    public static void main(String[] args)
    {
        int n = 4;
        System.out.println(countFriendsPairings(n));
    }
}

// This code is contributed by Ravi Kasha.

Python3

# Returns count of ways n people
# can remain single or paired up.
def countFriendsPairings(n):
    a, b, c = 1, 2, 0;
    if (n <= 2):
        return n;
    for i in range(3, n + 1):
        c = b + (i - 1) * a;
        a = b;
        b = c;
    return c;

# Driver code
n = 4;
print(countFriendsPairings(n));

# This code contributed by Rajput-Ji

C#

using System;

class GFG {
    // Returns count of ways n people
    // can remain single or paired up.
    static int countFriendsPairings(int n)
    {
        int a = 1, b = 2, c = 0;
        if (n <= 2) {
            return n;
        }
        for (int i = 3; i <= n; i++) {
            c = b + (i - 1) * a;
            a = b;
            b = c;
        }
        return c;
    }

    // Driver code
    public static void Main(String[] args)
    {
        int n = 4;
        Console.WriteLine(countFriendsPairings(n));
    }
}

// This code has been contributed by 29AjayKumar

PHP

<?php
    // Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings($n)
    {
        $a = 1;
        $b = 2;
        $c = 0;
        if ($n <= 2)
        {
            return $n;
        }
        for ($i = 3; $i <= $n; $i++)
        {
            $c = $b + ($i - 1) * $a;
            $a = $b;
            $b = $c;
        }
        return $c;
    }

    // Driver code
        $n = 4;
        print(countFriendsPairings($n));

// This code is contributed by mits
?>

Javascript

<script>
    // Returns count of ways n people
    // can remain single or paired up.
    function countFriendsPairings(n)
    {
        let a = 1, b = 2, c = 0;
        if (n <= 2) {
            return n;
        }
        for (let i = 3; i <= n; i++) {
            c = b + (i - 1) * a;
            a = b;
            b = c;
        }
        return c;
    }

    // Driver code
    let n = 4;
    document.write(countFriendsPairings(n));


    // This code is contributed by avanitrachhadiya2155
</script>

Output

10

Time Complexity : O(n) 
Auxiliary Space : O(1)

Another Approach: Since we can solve the above problem using maths, the solution below is done without using dynamic programming.

C++

// C++ soln using mathematical approach
#include <bits/stdc++.h>
using namespace std;

void preComputeFact(vector<long long int>& fact, int n)
{
    for(int i = 1; i <= n; i++)
        fact.push_back(fact[i - 1] * i);
}

// Returns count of ways n people
// can remain single or paired up.
int countFriendsPairings(vector<long long int> fact,
                         int n)
{
    int ones = n, twos = 1, ans = 0;

    while (ones >= 0)
    {

        // pow of 1 will always be one
        ans += fact[n] / (twos * fact[ones] *
               fact[(n - ones) / 2]);
        ones -= 2;
        twos *= 2;
    }
    return ans;
}

// Driver code
int main()
{
    vector<long long int> fact;
    fact.push_back(1);

    preComputeFact(fact, 100);
    int n = 4;

    cout << countFriendsPairings(fact, n) << endl;
    return 0;
}

// This code is contributed by rajsanghavi9.

Java

// Java soln using mathematical approach
import java.util.*;

class GFG{
static   Vector<Integer> fact;
static void preComputeFact( int n)
{
    for(int i = 1; i <= n; i++)
        fact.add(fact.elementAt(i - 1) * i);
}

// Returns count of ways n people
// can remain single or paired up.
static int countFriendsPairings(int n)
{
    int ones = n, twos = 1, ans = 0;

    while (ones >= 0)
    {

        // pow of 1 will always be one
        ans += fact.elementAt(n) / (twos * fact.elementAt(ones) *
               fact.elementAt((n - ones) / 2));
        ones -= 2;
        twos *= 2;
    }
    return ans;
}

// Driver code
public static void main(String[] args)
{
  fact = new Vector<>();
    fact.add(1);

    preComputeFact(100);
    int n = 4;

    System.out.print(countFriendsPairings(n) +"\n");
}
}

// This code is contributed by umadevi9616

Python3

# Python3 soln using mathematical approach
# factorial array is stored dynamically
fact = [1]
def preComputeFact(n):
    for i in range(1, n+1):
        fact.append((fact[i-1]*i))

# Returns count of ways n people
# can remain single or paired up.
def countFriendsPairings(n):
    ones = n
    twos = 1
    ans = 0
    while(ones >= 0):
        # pow of 1 will always be one
        ans = ans + (fact[n]//(twos*fact[ones]*fact[(n-ones)//2]))
        ones = ones - 2
        twos = twos * 2
    return(ans)


# Driver Code
# pre-compute factorial
preComputeFact(1000)
n = 4
print(countFriendsPairings(n))

# solution contributed by adarsh_007

C#

// C# program to implement the approach
using System;
using System.Collections.Generic;
public class GFG
{

  // initializing the fact list
  static List<int> fact = new List<int>();

  // computing the next n values of fact
  static void preComputeFact(int n)
  {
    for (int i = 1; i <= n; i++) {
      fact.Add(fact[i - 1] * i);
    }
  }

  // Returns count of ways n people
  // can remain single or paired up.
  static int countFriendsPairings(int n)
  {
    int ones = n;
    int twos = 1;
    int ans = 0;

    while (ones >= 0) {

      // pow of 1 will always be one
      ans += fact[n]
        / (twos * fact[ones]
           * fact[(n - ones) / 2]);
      ones -= 2;
      twos *= 2;
    }
    return ans;
  }

  // driver code
  static public void Main()
  {

    // initializing the first element of fact
    fact.Add(1);
    preComputeFact(100);
    int n = 4;
    Console.Write(countFriendsPairings(n));
  }
}

// this code is contributed by phasing17

Javascript

<script>

// Javascript soln using mathematical approach
// factorial array is stored dynamically

let fact = [1];

function preComputeFact(n)
{
    for(let i=1;i<n+1;i++)
    {
        fact.push((fact[i-1]*i));
    }
}

// Returns count of ways n people
// can remain single or paired up.
function countFriendsPairings(n)
{
    let ones = n
    let twos = 1;
    let ans = 0;
    while(ones >= 0)
    {
         // pow of 1 will always be one
        ans = ans + Math.floor(fact[n]/(twos*fact[ones]*
        fact[(n-ones)/2]))
        ones = ones - 2
        twos = twos * 2
    }
    return ans;
}

// Driver Code
// pre-compute factorial
preComputeFact(1000)
n = 4
document.write(countFriendsPairings(n))

// This code is contributed by ab2127

</script>

Output

10

Time Complexity:  O(n) 
Auxiliary Space: O(n)