Friedman Test

Friedman Test: It is a non-parametric test alternative to the one way ANOVA with repeated measures. It tries to determine if subjects changed significantly across occasions/conditions. For example:- Problem-solving ability of a set of people is the same or different in Morning, Afternoon, Evening. It is used to test for differences between groups when the dependent variable is ordinal. This test is particularly useful when the sample size is very small.

Elements of Friedman Test

• One group that is measured on three or more blocks of measures overtime/experimental conditions.
• One dependent variable which can be Ordinal, Interval or Ratio.

Assumptions of Friedman Test

• The group is a random sample from the population.
• Samples are not normally distributed.

Null and Alternate Hypothesis of Friedman Test

Null Hypothesis: There is no significant difference between the given conditions of measurement OR the probability distributions for all the conditions are the same. (Medians are same)

Alternate Hypothesis: At least 2 of them differ from each other.

H0 : M1 = M2 = M3 = ..... Mk  ; M= Median
H1 : At least two of them show significant difference.

Test Statistic for Friedman Test

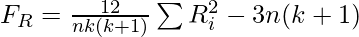
n = total number of subjects/participants.
k = total number of blocks to be measured.
Ri = sum of ranks of all subjects for a block i

Decision Rule for Friedman Test

You can make the decision on the basis of the below-mentioned rules-

1. Calculated Value vs Table Value: If F_R is greater than the critical value limits reject the Null Hypothesis. Otherwise, accept the Null Hypothesis.
2. P-Value Approach: Compare the P-Value with Alpha ( Level of Significance). If the p-value is less than or equal to alpha then reject the Null Hypothesis. 

Post Hoc Analysis: You can find out whether there is a difference in any given pair of experimental conditions if the null hypothesis is rejected using the Post Hoc analysis which can be done using Wilcoxon signed-rank test, Conover’s test etc.. In Wilcoxon test, you can get the results for all pairs also but you will have to make a Bonferroni correction which will change the level of significance to Given level of significance/total number of pairs.

Steps to perform Friedman Test: 

Let us take an example to understand how to perform this test.

Example: 7 random people were given 3 different drugs and for each person, the reaction time corresponding to the drugs were noted. Test the claim at the 5% significance level that all the 3 drugs have the same probability distribution.

	Drug A	Drug B	Drug C
1	1.24	1.50	1.62
2	1.71	1.85	2.05
3	1.37	2.12	1.68
4	2.53	1.87	2.62
5	1.23	1.34	1.51
6	1.94	2.33	2.86
7	1.72	1.43	2.86

Step 1: Define NULL and Alternate Hypothesis

H0 : All three drugs have the same probability distribution. MA = MB = MC
H1 : At least two of them differ from each other.

Step 2: State Alpha (Level of Significance)

Alpha = 0.05

Step 3: Calculate Degrees of Freedom

DF = K-1       ; K = number of blocks to be measured.
Here , DF = 3-1 =2.

Step 4:  Find out the Critical Chi-Square Value.

Use this table to find out the critical chi-square value for alpha = 0.05 and DF = 2.

X2 = 5.991

Step 5: State Decision Rule

You can check for any of the two rules – 

1) If FR is greater than 5.991 , reject the Null Hypothesis.

Step 6: Assign Ranks for the drugs corresponding to each person and find the sum. 

Ranks will be in Ascending order.

	Ranks
	Drug A	Drug B	Drug C
1	1	2	3
2	1	2	3
3	1	3	2
4	2	1	3
5	1	2	3
6	1	2	3
7	2	1	3
	∑ = 9	∑ = 13	∑ = 20

Note: If in the same row 2 or more columns have the same value then the rank assigned to them is the average of the ranks they get. For example: If a row has 2 columns with value x and the ranks which they get are 4 and 5. Then both the columns will be assigned with a rank of (4+5)/2 which is 4.5.

Step 7: Calculate Test Statistic

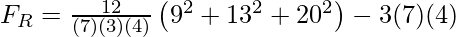
FR = 8.857

Step 8: State Results

Since FR is greater than 5.991 , We reject the Null Hypothesis.

Step 9: State Conclusion

All the three drugs do not have the same probability distribution.

You can apply the Post Hoc analysis with Wilcoxon Test to know which pairs have a significant difference between them.

Here,

Total number of pairs can be 3 (Drug A - Drug B , Drug B - Drug C , Drug A - Drug C).
The new level of significance to be considered for each pair will be 0.05/3 = 0.0166.

Implementation of Friedman Test using R

R

# R program to illustrate
# Friedman Test

#input the data
y <- matrix(c(1.24,1.50,1.62,
              1.71,1.85,2.05,
              1.37,2.12,1.68,
              2.53,1.87,2.62,
              1.23,1.34,1.51,
              1.94,2.33,2.86,
              1.72,1.43,2.86),
nrow = 7, byrow = TRUE,
dimnames = list(Person= as.character(1:7),Drugs = c("Drug A","Drug B","Drug C")))

#display the sample data
print(y)

Output:

R

#perform friedman test on the sample
result = friedman.test(y)
print(result)

Output:

As the p-value is less than the significance level (5%) it can be concluded that there are significant differences in the probability distribution.