Frequent Item set in Data set (Association Rule Mining)
Last Updated :
03 Feb, 2023
INTRODUCTION:
- Frequent item sets, also known as association rules, are a fundamental concept in association rule mining, which is a technique used in data mining to discover relationships between items in a dataset. The goal of association rule mining is to identify relationships between items in a dataset that occur frequently together.
- A frequent item set is a set of items that occur together frequently in a dataset. The frequency of an item set is measured by the support count, which is the number of transactions or records in the dataset that contain the item set. For example, if a dataset contains 100 transactions and the item set {milk, bread} appears in 20 of those transactions, the support count for {milk, bread} is 20.
- Association rule mining algorithms, such as Apriori or FP-Growth, are used to find frequent item sets and generate association rules. These algorithms work by iteratively generating candidate item sets and pruning those that do not meet the minimum support threshold. Once the frequent item sets are found, association rules can be generated by using the concept of confidence, which is the ratio of the number of transactions that contain the item set and the number of transactions that contain the antecedent (left-hand side) of the rule.
- Frequent item sets and association rules can be used for a variety of tasks such as market basket analysis, cross-selling and recommendation systems. However, it should be noted that association rule mining can generate a large number of rules, many of which may be irrelevant or uninteresting. Therefore, it is important to use appropriate measures such as lift and conviction to evaluate the interestingness of the generated rules.
Association Mining searches for frequent items in the data set. In frequent mining usually, interesting associations and correlations between item sets in transactional and relational databases are found. In short, Frequent Mining shows which items appear together in a transaction or relationship.
Need of Association Mining: Frequent mining is the generation of association rules from a Transactional Dataset. If there are 2 items X and Y purchased frequently then it’s good to put them together in stores or provide some discount offer on one item on purchase of another item. This can really increase sales. For example, it is likely to find that if a customer buys Milk and bread he/she also buys Butter. So the association rule is [‘milk]^[‘bread’]=>[‘butter’]. So the seller can suggest the customer buy butter if he/she buys Milk and Bread.
Important Definitions :
- Support : It is one of the measures of interestingness. This tells about the usefulness and certainty of rules. 5% Support means total 5% of transactions in the database follow the rule.
Support(A -> B) = Support_count(A ∪ B)
- Confidence: A confidence of 60% means that 60% of the customers who purchased a milk and bread also bought butter.
Confidence(A -> B) = Support_count(A ∪ B) / Support_count(A)
If a rule satisfies both minimum support and minimum confidence, it is a strong rule.
- Support_count(X): Number of transactions in which X appears. If X is A union B then it is the number of transactions in which A and B both are present.
- Maximal Itemset: An itemset is maximal frequent if none of its supersets are frequent.
- Closed Itemset: An itemset is closed if none of its immediate supersets have same support count same as Itemset.
- K- Itemset: Itemset which contains K items is a K-itemset. So it can be said that an itemset is frequent if the corresponding support count is greater than the minimum support count.
Example On finding Frequent Itemsets – Consider the given dataset with given transactions. 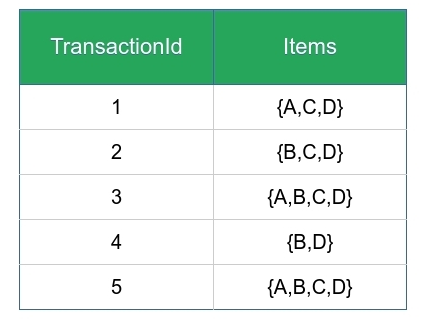
- Lets say minimum support count is 3
- Relation hold is maximal frequent => closed => frequent
1-frequent: {A} = 3; // not closed due to {A, C} and not maximal {B} = 4; // not closed due to {B, D} and no maximal {C} = 4; // not closed due to {C, D} not maximal {D} = 5; // closed item-set since not immediate super-set has same count. Not maximal
2-frequent: {A, B} = 2 // not frequent because support count < minimum support count so ignore {A, C} = 3 // not closed due to {A, C, D} {A, D} = 3 // not closed due to {A, C, D} {B, C} = 3 // not closed due to {B, C, D} {B, D} = 4 // closed but not maximal due to {B, C, D} {C, D} = 4 // closed but not maximal due to {B, C, D}
3-frequent: {A, B, C} = 2 // ignore not frequent because support count < minimum support count {A, B, D} = 2 // ignore not frequent because support count < minimum support count {A, C, D} = 3 // maximal frequent {B, C, D} = 3 // maximal frequent
4-frequent: {A, B, C, D} = 2 //ignore not frequent </
ADVANTAGES OR DISADVANTAGES:
Advantages of using frequent item sets and association rule mining include:
- Efficient discovery of patterns: Association rule mining algorithms are efficient at discovering patterns in large datasets, making them useful for tasks such as market basket analysis and recommendation systems.
- Easy to interpret: The results of association rule mining are easy to understand and interpret, making it possible to explain the patterns found in the data.
- Can be used in a wide range of applications: Association rule mining can be used in a wide range of applications such as retail, finance, and healthcare, which can help to improve decision-making and increase revenue.
- Handling large datasets: These algorithms can handle large datasets with many items and transactions, which makes them suitable for big-data scenarios.
Disadvantages of using frequent item sets and association rule mining include:
- Large number of generated rules: Association rule mining can generate a large number of rules, many of which may be irrelevant or uninteresting, which can make it difficult to identify the most important patterns.
- Limited in detecting complex relationships: Association rule mining is limited in its ability to detect complex relationships between items, and it only considers the co-occurrence of items in the same transaction.
- Can be computationally expensive: As the number of items and transactions increases, the number of candidate item sets also increases, which can make the algorithm computationally expensive.
- Need to define the minimum support and confidence threshold: The minimum support and confidence threshold must be set before the association rule mining process, which can be difficult and requires a good understanding of the data.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...