Form smallest number using indices of numbers chosen from Array with sum less than S
Last Updated :
16 Jun, 2021
Given an array arr[] and an integer S, the task is to choose the maximum count of numbers from the array such that the sum of numbers is less than S and form the smallest possible number using their indices
Note: Any element can be chosen any number of times.
Examples:
Input: arr[] = {3, 4, 2, 4, 6, 5, 4, 2, 3}, S = 13
Output: 133333
Explanation:
Elements chosen – 3 + 2 + 2 + 2 + 2 + 2 = 13
Therefore, Concatenation of indices – 133333
Input: arr[] = {18, 21, 22, 51, 13, 14, 17, 15, 17}, S = 50
Output: 115
Approach: The idea is to find the maximum count of the elements that can be chosen which can be computed for the number using
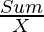
Finally, the minimum indices that can choose multiple times are computed by taking the minimum digit in the number for each digit place.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string max_number(int arr[], int sum)
{
int frac[9];
int maxi = INT_MIN;
string ans;
int pos;
for (int i = 0; i < 9; i++) {
frac[i] = sum / arr[i];
if (frac[i] > maxi) {
pos = i;
maxi = frac[i];
}
}
ans.insert(0,
string(maxi,
(pos + 1) + '0'));
sum -= maxi * arr[pos];
for (int i = 0; i < maxi; i++) {
for (int j = 1; j <= 9; j++) {
if (sum
+ arr[pos]
- arr[j - 1]
>= 0) {
ans[i] = (j + '0');
sum += arr[pos]
- arr[j - 1];
break;
}
}
}
if (maxi == 0) {
return 0;
}
else {
return ans;
}
}
int main()
{
int arr[9] = { 3, 4, 2, 4, 6,
5, 4, 2, 3 };
int s = 13;
cout << max_number(arr, s);
return 0;
}
|
Java
class GFG{
static String max_number(int arr[], int sum)
{
int frac[] = new int[9];
int maxi = Integer.MIN_VALUE;
StringBuilder ans = new StringBuilder();
int pos = 0;
for(int i = 0; i < 9; i++)
{
frac[i] = sum / arr[i];
if (frac[i] > maxi)
{
pos = i;
maxi = frac[i];
}
}
for(int i = 0; i < maxi; i++)
{
ans.append((char)((pos + 1) + '0'));
}
sum -= maxi * arr[pos];
for(int i = 0; i < maxi; i++)
{
for(int j = 1; j <= 9; j++)
{
if (sum + arr[pos] - arr[j - 1] >= 0)
{
ans.setCharAt(i, (char)(j + '0'));
sum += arr[pos] - arr[j - 1];
break;
}
}
}
if (maxi == 0)
{
return "0";
}
else
{
return ans.toString();
}
}
public static void main(String str[])
{
int arr[] = { 3, 4, 2, 4, 6,
5, 4, 2, 3 };
int s = 13;
System.out.println(max_number(arr, s));
}
}
|
Python3
def max_number(arr, sum):
frac = [0]*9
maxi = -10**9
pos = 0
for i in range(9):
frac[i] = sum // arr[i]
if (frac[i] > maxi):
pos = i
maxi = frac[i]
an = str((pos + 1)) * maxi
sum -= maxi * arr[pos]
ans = [i for i in an]
for i in range(maxi):
for j in range(1, 10):
if (sum + arr[pos] - arr[j - 1] >= 0):
ans[i] = str(j)
sum += arr[pos] - arr[j - 1]
break
if (maxi == 0):
return 0
else:
return "".join(ans)
if __name__ == '__main__':
arr = [ 3, 4, 2, 4, 6,
5, 4, 2, 3 ]
s = 13
print(max_number(arr, s))
|
C#
using System;
using System.Text;
class GFG{
static String max_number(int []arr,
int sum)
{
int []frac = new int[9];
int maxi = int.MinValue;
StringBuilder ans =
new StringBuilder();
int pos = 0;
for(int i = 0; i < 9; i++)
{
frac[i] = sum / arr[i];
if (frac[i] > maxi)
{
pos = i;
maxi = frac[i];
}
}
for(int i = 0; i < maxi; i++)
{
ans.Append((char)((pos + 1) + '0'));
}
sum -= maxi * arr[pos];
for(int i = 0; i < maxi; i++)
{
for(int j = 1; j <= 9; j++)
{
if (sum + arr[pos] -
arr[j - 1] >= 0)
{
ans[i] = (char)(j + '0');
sum += arr[pos] - arr[j - 1];
break;
}
}
}
if (maxi == 0)
{
return "0";
}
else
{
return ans.ToString();
}
}
public static void Main(String []str)
{
int []arr = {3, 4, 2, 4, 6,
5, 4, 2, 3};
int s = 13;
Console.WriteLine(max_number(arr, s));
}
}
|
Javascript
<script>
function max_number(arr,sum)
{
let frac = new Array(9);
let maxi = Number.MIN_VALUE;
let ans = [];
let pos = 0;
for(let i = 0; i < 9; i++)
{
frac[i] = Math.floor(sum / arr[i]);
if (frac[i] > maxi)
{
pos = i;
maxi = frac[i];
}
}
for(let i = 0; i < maxi; i++)
{
ans.push(String.fromCharCode((pos + 1) + '0'.charCodeAt(0)));
}
sum -= maxi * arr[pos];
for(let i = 0; i < maxi; i++)
{
for(let j = 1; j <= 9; j++)
{
if (sum + arr[pos] - arr[j - 1] >= 0)
{
ans[i] = String.fromCharCode((j + '0'.charCodeAt(0)));
sum += arr[pos] - arr[j - 1];
break;
}
}
}
if (maxi == 0)
{
return "0";
}
else
{
return ans.join("");
}
}
let arr = [3, 4, 2, 4, 6,
5, 4, 2, 3];
let s = 13;
document.write(max_number(arr, s));
</script>
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...