Finding Inverse of a Square Matrix using Cayley Hamilton Theorem in MATLAB
Last Updated :
18 Apr, 2022
Matrix is the set of numbers arranged in rows & columns in order to form a Rectangular array. Here, those numbers are called the entries or elements of that matrix. A Rectangular array of (m*n) numbers in the form of ‘m’ horizontal lines (rows) & ‘n’ vertical lines (called columns), is called a matrix of order m by n, which is written as m × n matrix.
Note: If m=n i.e., Number of Rows = Number of Columns in a Matrix ‘A’, then ‘A’ is said to be a Square Matrix of order ‘n’.
The inverse of a Square Matrix:
If ‘A’ is a non-singular (|A| ≠ 0) square matrix of order ‘n’, then there exists an n x n matrix A-1, which is called the inverse matrix of ‘A’, which satisfies the following property:
AA-1 = A-1A = In, where In is the Identity matrix of order n
We can Find Inverse of a Square Matrix using various methods like:
- Cayley-Hamilton Method
- Gaussian Elimination
- Newton’s Method
- Eigen Decomposition Method
Cayley-Hamilton’s theorem:
In the Domain of Linear Algebra, According to Cayley-Hamilton’s theorem, every square matrix ‘A’ of order ‘n’ satisfies its own characteristic equation, which is given by:
|A-λIn| = 0
Here 'In' is the Identity Matrix
of Order 'n' (same as that of A's Order)
and 'λ' is some Real Constant.
Expanding the above characteristic equation of ‘A’, we get:
λn + C1λn-1 + C2λn-2 + . . . + CnIn = 0,
where C1, C2, . . . , Cn are Real Constants.
According to Cayley-Hamilton’s theorem, The above characteristic equation of ‘A’ is satisfied by itself, Hence we have:
An + C1An-1 + C2An-2 + . . . + CnIn = 0 ,
where C1, C2, . . . , Cn are Real Constants.
Steps to Find Inverse of a Square Matrix using Cayley Hamilton theorem:
Step 1: For a Given Non-singular Square Matrix ‘A’ of order ‘n’, Find its Characteristic equation |A-λIn| = 0.
Expand the Determinant such that it is reduced in the below format:
λn + C1λn-1 + C2λn-2 + . . . + CnIn = 0,
where C1, C2, . . . , Cn are Real Constants.
Step 2: As per Cayley-Hamilton’s theorem, the above Characteristic equation of ‘A’ is satisfied by itself, Hence:
An + C1An-1 + C2An-2 + . . . + CnIn = 0
Step 3: Multiplying by A-1 on Both Sides of the above Equation reduces it to:
An-1 + C1An-2 + C2An-3 + . . . Cn-1In + CnA-1 = 0
Step 4: Find A-1 by simplifying and reordering the terms of the above equation, then A-1 is:
A-1 = (-1/Cn)[ An-1 + C1An-2 + C2An-3 + . . . Cn-1In ]
MATLAB Functions used in the Below Code are:
- disp(“txt”): This Method displays the message-‘txt’ to the User.
- input(“txt”): This Method displays the message-‘txt’ and waits for the user to input a value and press the Return key.
- poly(A): This method returns the n+1 coefficients of the Characteristic polynomial of the matrix ‘A’ of order ‘n’.
- length(X): This method returns the number of elements of the vector ‘X’.
- round(x): This Method rounds ‘x’ to its nearest integer.
Example:
Matlab
clear all
clc
disp("Finding Inverse of a Square Matrix using
Cayley Hamilton theorem in MATLAB | GeeksforGeeks")
A=input('Enter the Matrix A: ');
cf=poly(A);
n=length(cf);
inverse = cf(1)*A^(n-2);
for i=2:n-1
inverse=inverse+cf(i)*A^(n-i-1);
end
if round(cf(n))==0
disp('Inverse of A does not exist as it is a singular matrix..')
else
inverse=inverse/(-cf(n));
disp('Inverse of A: ')
disp(inverse)
end
|
Output:
Input matrix:
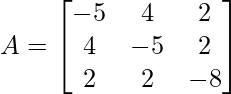
Input matrix:
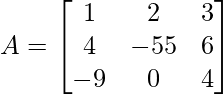
Input matrix:
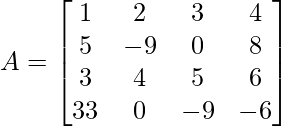
Share your thoughts in the comments
Please Login to comment...