Finding Derivative with Fundamental Theorem of Calculus
Last Updated :
24 Jun, 2021
Integrals are the reverse process of differentiation. They are also called anti-derivatives and are used to find the areas and volumes of the arbitrary shapes for which there are no formulas available to us. Indefinite integrals simply calculate the anti-derivative of the function, while the definite integrals have limits and usually denote the area under the curve. The fundamental theorem of calculus relates the integral rules with derivatives and chain rules. It is used to solving hard problems in integration. Let’s look at this theorem.
Applying the Fundamental Theorem of Calculus
Consider a function f(x) to be a function which is continuous and differentiable in the given interval [a, b]. The definite integral between these limits is denoted by 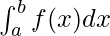 . This is defined as the area enclosed by the function f(x) and x-axis between the limits x = a and x = b. This definite integral can be converted into a function by varying the upper bound of the limit. This function can be re-written as,
. This is defined as the area enclosed by the function f(x) and x-axis between the limits x = a and x = b. This definite integral can be converted into a function by varying the upper bound of the limit. This function can be re-written as,
Let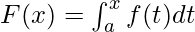 . Now geometrically, this function gives us the area under the same curve but from x = a to x, where x lies between the boundaries of the limits. The figure below shows this function:
. Now geometrically, this function gives us the area under the same curve but from x = a to x, where x lies between the boundaries of the limits. The figure below shows this function:

Now at x = a, 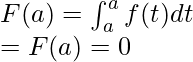
The fundamental theorem enables us to calculate the derivatives of the given function.
Fundamental Theorem of Calculus – Part I
For a function f which is continuous and differentiable on the interval [a, b], suppose 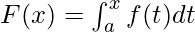 . Then, F is a differentiable function on (a, b), and
. Then, F is a differentiable function on (a, b), and
F'(x) = f(x)
This theorem seems trivial but has very far-reaching implications. There is a function f(x) = x2 + sin(x),
Given, F(x) = 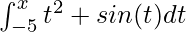
According to the fundamental theorem mentioned above,
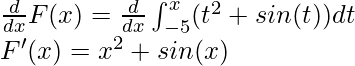
This theorem can be used to derive a popular result,
Suppose there is a definite integral 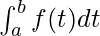 . Also, let’s say F(x) =
. Also, let’s say F(x) = 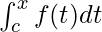 .
.
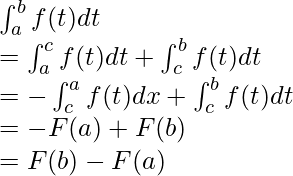
This is the second part of the Fundamental Theorem of Calculus.
Fundamental Theorem of Calculus – Part II
For a function f which is continuous and differentiable on the interval [a, b], let F be any anti-derivative of the given function. Then,
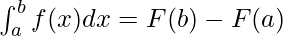
Applying Fundamental Theorem with Chain Rule
Hard problems of definite integrals can be solved by combining the chain rule and the fundamental theorem of calculus. For example,
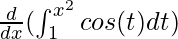
To solve such problems, we need a more generalized version of the fundamental theorem.
For a function f which is continuous and two other functions g and h which are differentiable,
![Rendered by QuickLaTeX.com \frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ebb3d8b6a1be7308c74fdac3bc5baf3_l3.png)
Let’s look at some problems related to these concepts.
Sample Problems
Question 1: Given the following function F(x), calculate its derivative.
F(x) = 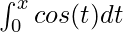
Solution:
Given: F(x) = 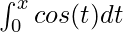
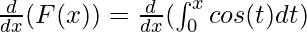
This can be solved using the fundamental theorem of calculus part – I
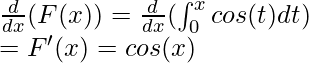
Question 2: Given the following function F(x), calculate its derivative.
F(x) = 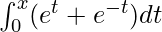
Solution:
Given: F(x) = 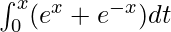
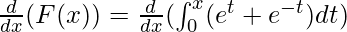
This can be solved using the fundamental theorem of calculus part – I
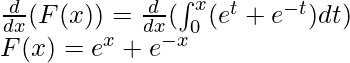
Question 3: Given the following function F(x), calculate its derivative.
F(x) = 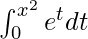
Solution:
Given: F(x) = 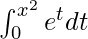
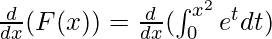
This can be solved using the generalized form of the fundamental theorem of calculus part – I. It states that,
![Rendered by QuickLaTeX.com \frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ebb3d8b6a1be7308c74fdac3bc5baf3_l3.png)
Here, f(t) = et, h(x) = x2 and g(x) = 0
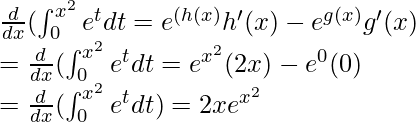
Question 4: Given the following function F(x), calculate its derivative.
F(x) = 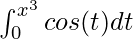
Solution:
Given: F(x) = 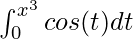
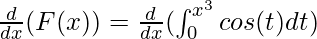
This can be solved using the generalized form of the fundamental theorem of calculus part – I. It states that,
![Rendered by QuickLaTeX.com \frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ebb3d8b6a1be7308c74fdac3bc5baf3_l3.png)
Here, f(t) = cos(t), h(x) = x3 and g(x) = 0
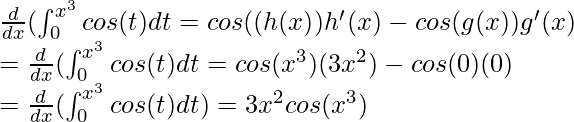
Question 5: Given the following function F(x), calculate its derivative.
F(x) = 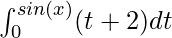
Solution:
Given: F(x) = 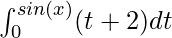
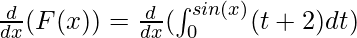
This can be solved using the generalized form of the fundamental theorem of calculus part – I. It states that,
![Rendered by QuickLaTeX.com \frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ebb3d8b6a1be7308c74fdac3bc5baf3_l3.png)
Here, f(t) = t + 2, g(x) = 0 and h(x) = sin(x)
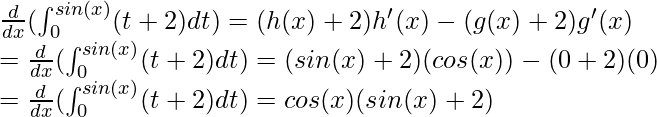
Question 6: Given the following function F(x), calculate its derivative.
F(x) = 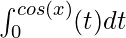
Solution:
Given: F(x) = 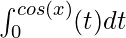
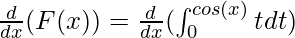
This can be solved using the generalized form of the fundamental theorem of calculus part – I. It states that,
![Rendered by QuickLaTeX.com \frac{d}{dx}\int^{h(x)}_{g(x)}f(s)ds = \frac{d}{dx}[F(h(x)) - F(g(x))] \\ = F'(h(x))h'(x) - F'(g(x))g'(x) \\ = f((h(x))h'(x) - f(g(x))g'(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ebb3d8b6a1be7308c74fdac3bc5baf3_l3.png)
Here, f(t) = t, g(x) = 0 and h(x) = cos(x)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...