Finding the best fit rectangle that covers a given point
Last Updated :
25 Oct, 2022
We are provided with a 2D plane and a point (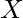 ,
,  ). We have to find a rectangle (
). We have to find a rectangle ( ,
,  ,
, 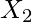 ,
, 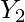 ) such that it
) such that it
encompasses the given point (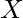 ,
,  ). The rectangle chosen must satisfy the given condition
). The rectangle chosen must satisfy the given condition 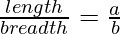 . If
. If
multiple rectangles are possible the we must choose the one with the least Euclid distance between the center of the rectangle and the point (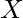 ,
,  ).
).

Image Source – codeforces
Examples :
Input : 70 10 20 5 5 3
Output :12 0 27 9
Input :100 100 32 63 2 41
Output :30 18 34 100
The logic behind the problem is as follows. First of all we reduce 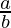 to lowest irreducible form by dividing a and b by
to lowest irreducible form by dividing a and b by 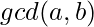 . We think of the problem in two separate dimensions
. We think of the problem in two separate dimensions 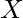 and
and  independently. We find out the
independently. We find out the 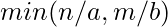 after dividing a and b by their gcd to find the maximum distance that we can cover safely by staying in the range of
after dividing a and b by their gcd to find the maximum distance that we can cover safely by staying in the range of 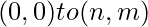 . Since we have to find rectangle with minimum distance of its center from the point (
. Since we have to find rectangle with minimum distance of its center from the point (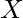 ,
,  ), therefore we start with the assumption that point (
), therefore we start with the assumption that point (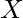 ,
,  ) is our center. Then we find
) is our center. Then we find  and
and 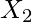 by subtracting and adding half of length to
by subtracting and adding half of length to 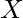 . If either
. If either  or
or 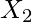 goes out of range then we shift the coordinates accordingly to bring it inside the range
goes out of range then we shift the coordinates accordingly to bring it inside the range 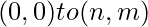 . Similarly we proceed to calculate
. Similarly we proceed to calculate  and
and 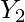 .
.
For the first example according to above logic the answer comes out to be 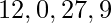 .
.
C++
#include <cmath>
#include <iostream>
using namespace std;
int gcd(int a, int b)
{
if (a == 0)
return b;
else
return gcd(b % a, a);
}
void solve(int n, int m, int x, int y, int a, int b)
{
int k, g;
int x1, y1, x2, y2;
g = gcd(a, b);
a /= g;
b /= g;
k = min(n / a, m / b);
x1 = x - (k * a - k * a / 2);
x2 = x + k * a / 2;
y1 = y - (k * b - k * b / 2);
y2 = y + k * b / 2;
if (x1 < 0) {
x2 -= x1;
x1 = 0;
}
if (x2 > n) {
x1 -= x2 - n;
x2 = n;
}
if (y1 < 0) {
y2 -= y1;
y1 = 0;
}
if (y2 > m) {
y1 -= y2 - m;
y2 = m;
}
cout << x1 << " " << y1 << " " << x2 << " " << y2
<< endl;
}
int main()
{
int n = 70, m = 10, x = 20, y = 5, a = 5, b = 3;
solve(n, m, x, y, a, b);
return 0;
}
|
Java
class GFG {
public static int gcd(int a, int b)
{
if (a == 0)
return b;
else
return gcd(b % a, a);
}
public static void solve(int n, int m, int x, int y,
int a, int b)
{
int k, g;
int x1, y1, x2, y2;
g = gcd(a, b);
a /= g;
b /= g;
k = Math.min(n / a, m / b);
x1 = x - (k * a - k * a / 2);
x2 = x + k * a / 2;
y1 = y - (k * b - k * b / 2);
y2 = y + k * b / 2;
if (x1 < 0) {
x2 -= x1;
x1 = 0;
}
if (x2 > n) {
x1 -= x2 - n;
x2 = n;
}
if (y1 < 0) {
y2 -= y1;
y1 = 0;
}
if (y2 > m) {
y1 -= y2 - m;
y2 = m;
}
System.out.println(x1 + " " + y1 + " " + x2 + " "
+ y2);
}
public static void main(String args[])
{
int n = 70, m = 10;
int x = 20, y = 5;
int a = 5, b = 3;
solve(n, m, x, y, a, b);
}
}
|
Python 3
def gcd(a, b):
if (a == 0):
return b
else:
return gcd(b % a, a)
def solve(n, m, x, y, a, b):
g = int(gcd(a, b))
a /= g
b /= g
k = int(min(n / a, m / b))
x1 = int(x - (k * a - k * a / 2))
x2 = int(x + k * a / 2)
y1 = int(y - (k * b - k * b / 2))
y2 = int(y + k * b / 2)
if (int(x1) < 0):
x2 -= x1
x1 = 0
if (int(x2) > n):
x1 -= x2 - n
x2 = n
if (int(y1) < 0):
y2 -= y1
y1 = 0
if (int(y2) > m):
y1 -= y2 - m
y2 = m
print(x1, " ", y1, " ", x2, " ", y2, sep="")
n = 70
m = 10
x = 20
y = 5
a = 5
b = 3
solve(n, m, x, y, a, b)
|
C#
using System;
class GFG {
public static int gcd(int a, int b)
{
if (a == 0)
return b;
else
return gcd(b % a, a);
}
public static void solve(int n, int m, int x, int y,
int a, int b)
{
int k, g;
int x1, y1, x2, y2;
g = gcd(a, b);
a /= g;
b /= g;
k = Math.Min(n / a, m / b);
x1 = x - (k * a - k * a / 2);
x2 = x + k * a / 2;
y1 = y - (k * b - k * b / 2);
y2 = y + k * b / 2;
if (x1 < 0) {
x2 -= x1;
x1 = 0;
}
if (x2 > n) {
x1 -= x2 - n;
x2 = n;
}
if (y1 < 0) {
y2 -= y1;
y1 = 0;
}
if (y2 > m) {
y1 -= y2 - m;
y2 = m;
}
Console.Write(x1 + " " + y1 + " " + x2 + " " + y2);
}
public static void Main()
{
int n = 70, m = 10;
int x = 20, y = 5;
int a = 5, b = 3;
solve(n, m, x, y, a, b);
}
}
|
PHP
<?php
function gcd($a, $b)
{
if ($a == 0)
return $b;
else
return gcd($b % $a, $a);
}
function solve($n, $m, $x, $y, $a, $b)
{
$k; $g;
$x1; $y1; $x2; $y2;
$g = gcd($a, $b);
$a /= $g;
$b /= $g;
$k = min($n / $a, $m / $b);
$x1 = $x - ($k * $a - $k * $a / 2);
$x2 = $x + $k * $a / 2;
$y1 = $y - ($k * $b - $k * $b / 2);
$y2 = $y + $k * $b / 2;
if ($x1 < 0)
{
$x2 -= $x1;
$x1 = 0;
}
if ($x2 > $n)
{
$x1 -= $x2 - $n;
$x2 = $n;
}
if ($y1 < 0)
{
$y2 -= $y1;
$y1 = 0;
}
if ($y2 > $m)
{
$y1 -= $y2 - $m;
$y2 = $m;
}
echo $x1, " ", $y1, " ",
$x2, " ", $y2, "\n";
}
$n = 70; $m = 10; $x = 20;
$y = 5; $a = 5; $b = 3;
solve($n, $m, $x, $y, $a, $b);
?>
|
Javascript
<script>
function gcd(a, b)
{
if (a == 0)
return b;
else
return gcd(b % a, a);
}
function solve(n, m, x, y, a, b)
{
let k, g;
let x1, y1, x2, y2;
g = gcd(a, b);
a = a / g;
b = b / g;
k = Math.min(parseInt(n / a, 10), parseInt(m / b, 10));
x1 = x - (k * a - k * parseInt(a / 2, 10));
x2 = x + k * parseInt(a / 2, 10);
y1 = y - (k * b - k * parseInt(b / 2, 10));
y2 = y + k * parseInt(b / 2, 10);
if (x1 < 0) {
x2 -= x1;
x1 = 0;
}
if (x2 > n) {
x1 -= x2 - n;
x2 = n;
}
x1 += 1; x2 += 1;
if (y1 < 0) {
y2 -= y1;
y1 = 0;
}
if (y2 > m) {
y1 -= y2 - m;
y2 = m;
}
document.write(x1 + " " + y1 + " " + x2 + " " + y2);
}
let n = 70, m = 10;
let x = 20, y = 5;
let a = 5, b = 3;
solve(n, m, x, y, a, b);
</script>
|
Time complexity: O(log(min(a,b)))
Auxiliary space: O(log(min(a,b))
Share your thoughts in the comments
Please Login to comment...