Finding Additional functional dependencies in a relation

A functional dependency is simply a constraint between two sets of attributes from the database. A functional dependency is used in normalization. A functional dependency is denoted by an arrow → .The functional dependency of A on B is represented by A → B. Functional Dependency plays a vital role in finding the difference between good and bad database design.

A→B

Above Functional dependency is pronounced as :

1. A determines B
2. A functionally determines B
3. B is functionally dependent on A
4. For a given value of A, we can functionally determine the value of B.

A and B can be a set of attributes, they need not be single attributes always.

Example : 
AB→B,  A→ ACB etc. 

With a given relation, we are also given a set of Functional dependencies most of the time according to the semantics of the database design. Most interesting thing is that we can yield more additional functional dependencies by applying some rules on the functional dependencies given. Example: A relation R(AB) is given with functional dependencies F : { A→B, B→A }. Find out the additional functional dependencies derivable from the given functional dependencies on the relation R. Explanation: Step-1: Finding out the set of possible functional dependencies: Assume the functional dependency as A→B. A functional dependency will have Left side that is A here and Right side that is B here. 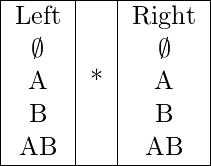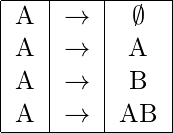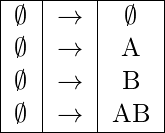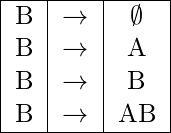So the valid attribute we can have in either side is given below: Therefore, number of functional dependencies possible = 4*4 = 16 Step-2: Listing out all possible functional dependencies with 2 attributes AB of the relation R: Following are the list of all 16 possible functional dependencies with 2 attributes AB of the relation R: 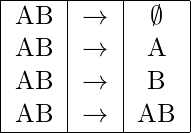Step-3: Checking if the possible functional dependencies are derivable or not: In this step, we check if the possible functional dependencies are derivable by a given set of functional dependencies or not, by using the closure set of attributes. Φ → Φ : derivable since its a trivial functional dependency. A→Φ : derivable since phi is a subset of A A→A : derivable since its a trivial functional dependency. A→B : derivable from the given functional dependency A→B. A→AB : derivable since the closure set of A gives AB. B→Φ : derivable since phi is a subset of B B→A : derivable from the given functional dependency B→A. B→B : derivable since its a trivial functional dependency. B→AB : derivable since the closure set of B gives AB. AB→Φ : derivable since its a trivial functional dependency. AB→A : derivable since its a trivial functional dependency. AB→B : derivable since its a trivial functional dependency. AB→AB : derivable since its a trivial functional dependency. The rest of the possible dependencies are not valid. Therefore, the total number of additional functional dependencies that can be determined by the given functional dependencies A→B and B→A on relation R is 13, including A→B, B→A are listed below :

Φ→Φ, A→Φ, A→A, A→B, A→AB, B→Φ, B→A, B→B, B→AB, AB→Φ, AB→A, AB→B, AB→AB