Find whether there is path between two cells in matrix

Given N X N matrix filled with 1, 0, 2, 3. Find whether there is a path possible from source to destination, traversing through blank cells only. You can traverse up, down, right, and left. 

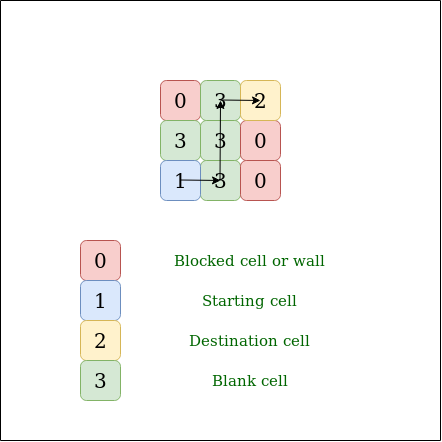
• A value of cell 1 means Source.
• A value of cell 2 means Destination.
• A value of cell 3 means Blank cell.
• A value of cell 0 means Blank Wall.

Note: there are an only a single source and single destination(sink). 

Examples:

Input:
M[3][3] = {{ 0, 3, 2 }, 
{ 3, 3, 0 }, 
{ 1, 3, 0 }}; 
Output : Yes 
Explanation:

Input:
M[4][4] = {{ 0, 3, 1, 0 }, 
{ 3, 0, 3, 3 }, 
{ 2, 3, 0, 3 }, 
{ 0, 3, 3, 3 }}; 
Output: Yes 
Explanation:

Find whether there is path between two cells in matrix using Recursion:

The idea is to find the source index of the cell in each matrix and then recursively find a path from the source index to the destination in the matrix. The algorithm involves recursively finding all the paths until a final path is found to the destination.

Follow the steps below to solve the problem:

• Traverse the matrix and find the starting index of the matrix.
• Create a recursive function that takes the index and visited matrix.
• Mark the current cell and check if the current cell is a destination or not. If the current cell is the destination, return true.
• Call the recursion function for all adjacent empty and unvisited cells.
• If any of the recursive functions returns true then unmark the cell and return true else unmark the cell and return false.

Below is the implementation of the above approach.

C++

// C++ program to find path between two
// cell in matrix
#include <bits/stdc++.h>
using namespace std;

#define N 4

// Method for checking boundaries
bool isSafe(int i, int j, int matrix[][N])
{
    if (i >= 0 && i < N && j >= 0 && j < N)
        return true;
    return false;
}

// Returns true if there is a
// path from a source (a
// cell with value 1) to a
// destination (a cell with
// value 2)
bool isaPath(int matrix[][N], int i, int j,
            bool visited[][N])
{
    // Checking the boundaries, walls and
    // whether the cell is unvisited
    if (isSafe(i, j, matrix) && matrix[i][j] != 0
        && !visited[i][j]) {
        // Make the cell visited
        visited[i][j] = true;

        // if the cell is the required
        // destination then return true
        if (matrix[i][j] == 2)
            return true;

        // traverse up
        bool up = isaPath(matrix, i - 1, j, visited);

        // if path is found in up
        // direction return true
        if (up)
            return true;

        // traverse left
        bool left = isaPath(matrix, i, j - 1, visited);

        // if path is found in left
        // direction return true
        if (left)
            return true;

        // traverse down
        bool down = isaPath(matrix, i + 1, j, visited);

        // if path is found in down
        // direction return true
        if (down)
            return true;

        // traverse right
        bool right = isaPath(matrix, i, j + 1, visited);

        // if path is found in right
        // direction return true
        if (right)
            return true;
    }

    // no path has been found
    return false;
}

// Method for finding and printing
// whether the path exists or not
void isPath(int matrix[][N])
{

    // Defining visited array to keep
    // track of already visited indexes
    bool visited[N][N];
    memset(visited, 0, sizeof(visited));

    // Flag to indicate whether the
    // path exists or not
    bool flag = false;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            // if matrix[i][j] is source
            // and it is not visited
            if (matrix[i][j] == 1 && !visited[i][j])

                // Starting from i, j and
                // then finding the path
                if (isaPath(matrix, i, j, visited)) {

                    // if path exists
                    flag = true;
                    break;
                }
        }
    }
    if (flag)
        cout << "YES";
    else
        cout << "NO";
}

// Driver program to
// check above function
int main()
{
    int matrix[N][N] = { { 0, 3, 0, 1 },
                         { 3, 0, 3, 3 },
                         { 2, 3, 3, 3 },
                         { 0, 3, 3, 3 } };

    // calling isPath method
    isPath(matrix);
    return 0;
}

// This code is contributed by sudhanshugupta2019a.

Java

// Java program to find path between two
// cell in matrix

import java.io.*;

class Path {

    // Method for finding and printing
    // whether the path exists or not
    public static void isPath(int matrix[][], int n)
    {
        // Defining visited array to keep
        // track of already visited indexes
        boolean visited[][] = new boolean[n][n];

        // Flag to indicate whether the
        // path exists or not
        boolean flag = false;

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                // if matrix[i][j] is source
                // and it is not visited
                if (matrix[i][j] == 1 && !visited[i][j])

                    // Starting from i, j and
                    // then finding the path
                    if (isPath(matrix, i, j, visited)) {
                        // if path exists
                        flag = true;
                        break;
                    }
            }
        }
        if (flag)
            System.out.println("YES");
        else
            System.out.println("NO");
    }

    // Method for checking boundaries
    public static boolean isSafe(int i, int j,
                                 int matrix[][])
    {

        if (i >= 0 && i < matrix.length && j >= 0
            && j < matrix[0].length)
            return true;
        return false;
    }

    // Returns true if there is a
    // path from a source (a
    // cell with value 1) to a
    // destination (a cell with
    // value 2)
    public static boolean isPath(int matrix[][], int i,
                                 int j, boolean visited[][])
    {

        // Checking the boundaries, walls and
        // whether the cell is unvisited
        if (isSafe(i, j, matrix) && matrix[i][j] != 0
            && !visited[i][j]) {
            // Make the cell visited
            visited[i][j] = true;

            // if the cell is the required
            // destination then return true
            if (matrix[i][j] == 2)
                return true;

            // traverse up
            boolean up = isPath(matrix, i - 1, j, visited);

            // if path is found in up
            // direction return true
            if (up)
                return true;

            // traverse left
            boolean left
                = isPath(matrix, i, j - 1, visited);

            // if path is found in left
            // direction return true
            if (left)
                return true;

            // traverse down
            boolean down
                = isPath(matrix, i + 1, j, visited);

            // if path is found in down
            // direction return true
            if (down)
                return true;

            // traverse right
            boolean right
                = isPath(matrix, i, j + 1, visited);

            // if path is found in right
            // direction return true
            if (right)
                return true;
        }
        // no path has been found
        return false;
    }

    // driver program to
    // check above function
    public static void main(String[] args)
    {

        int matrix[][] = { { 0, 3, 0, 1 },
                           { 3, 0, 3, 3 },
                           { 2, 3, 3, 3 },
                           { 0, 3, 3, 3 } };

        // calling isPath method
        isPath(matrix, 4);
    }
}

/* This code is contributed by Madhu Priya */

Python3

# Python3 program to find
# path between two cell in matrix

# Method for finding and printing
# whether the path exists or not


def isPath(matrix, n):

    # Defining visited array to keep
    # track of already visited indexes
    visited = [[False for x in range(n)]
               for y in range(n)]

    # Flag to indicate whether the
    # path exists or not
    flag = False

    for i in range(n):
        for j in range(n):

            # If matrix[i][j] is source
            # and it is not visited
            if (matrix[i][j] == 1 and not
                    visited[i][j]):

                # Starting from i, j and
                # then finding the path
                if (checkPath(matrix, i,
                              j, visited)):

                    # If path exists
                    flag = True
                    break
    if (flag):
        print("YES")
    else:
        print("NO")

# Method for checking boundaries


def isSafe(i, j, matrix):

    if (i >= 0 and i < len(matrix) and
            j >= 0 and j < len(matrix[0])):
        return True
    return False

# Returns true if there is a
# path from a source(a
# cell with value 1) to a
# destination(a cell with
# value 2)


def checkPath(matrix, i, j,
              visited):

    # Checking the boundaries, walls and
    # whether the cell is unvisited
    if (isSafe(i, j, matrix) and
        matrix[i][j] != 0 and not
            visited[i][j]):

        # Make the cell visited
        visited[i][j] = True

        # If the cell is the required
        # destination then return true
        if (matrix[i][j] == 2):
            return True

        # traverse up
        up = checkPath(matrix, i - 1,
                       j, visited)

        # If path is found in up
        # direction return true
        if (up):
            return True

        # Traverse left
        left = checkPath(matrix, i,
                         j - 1, visited)

        # If path is found in left
        # direction return true
        if (left):
            return True

        # Traverse down
        down = checkPath(matrix, i + 1,
                         j, visited)

        # If path is found in down
        # direction return true
        if (down):
            return True

        # Traverse right
        right = checkPath(matrix, i,
                          j + 1, visited)

        # If path is found in right
        # direction return true
        if (right):
            return True

    # No path has been found
    return False


# Driver code
if __name__ == "__main__":

    matrix = [[0, 3, 0, 1],
              [3, 0, 3, 3],
              [2, 3, 3, 3],
              [0, 3, 3, 3]]

    # calling isPath method
    isPath(matrix, 4)

# This code is contributed by Chitranayal

C#

// C# program to find path between two
// cell in matrix
using System;

class GFG {

    // Method for finding and printing
    // whether the path exists or not
    static void isPath(int[, ] matrix, int n)
    {

        // Defining visited array to keep
        // track of already visited indexes
        bool[, ] visited = new bool[n, n];

        // Flag to indicate whether the
        // path exists or not
        bool flag = false;

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {

                // If matrix[i][j] is source
                // and it is not visited
                if (matrix[i, j] == 1 && !visited[i, j])

                    // Starting from i, j and
                    // then finding the path
                    if (isPath(matrix, i, j, visited)) {

                        // If path exists
                        flag = true;
                        break;
                    }
            }
        }
        if (flag)
            Console.WriteLine("YES");
        else
            Console.WriteLine("NO");
    }

    // Method for checking boundaries
    public static bool isSafe(int i, int j, int[, ] matrix)
    {
        if (i >= 0 && i < matrix.GetLength(0) && j >= 0
            && j < matrix.GetLength(1))
            return true;

        return false;
    }

    // Returns true if there is a path from
    // a source (a cell with value 1) to a
    // destination (a cell with value 2)
    public static bool isPath(int[, ] matrix, int i, int j,
                              bool[, ] visited)
    {

        // Checking the boundaries, walls and
        // whether the cell is unvisited
        if (isSafe(i, j, matrix) && matrix[i, j] != 0
            && !visited[i, j]) {

            // Make the cell visited
            visited[i, j] = true;

            // If the cell is the required
            // destination then return true
            if (matrix[i, j] == 2)
                return true;

            // Traverse up
            bool up = isPath(matrix, i - 1, j, visited);

            // If path is found in up
            // direction return true
            if (up)
                return true;

            // Traverse left
            bool left = isPath(matrix, i, j - 1, visited);

            // If path is found in left
            // direction return true
            if (left)
                return true;

            // Traverse down
            bool down = isPath(matrix, i + 1, j, visited);

            // If path is found in down
            // direction return true
            if (down)
                return true;

            // Traverse right
            bool right = isPath(matrix, i, j + 1, visited);

            // If path is found in right
            // direction return true
            if (right)
                return true;
        }

        // No path has been found
        return false;
    }

    // Driver code
    static void Main()
    {
        int[, ] matrix = { { 0, 3, 0, 1 },
                           { 3, 0, 3, 3 },
                           { 2, 3, 3, 3 },
                           { 0, 3, 3, 3 } };

        // Calling isPath method
        isPath(matrix, 4);
    }
}

// This code is contributed by divyeshrabadiya07

Javascript

<script>

// JavaScript program to find path between two
// cell in matrix

    // Method for finding and printing
    // whether the path exists or not
function isPath(matrix,n)
{

    // Defining visited array to keep
        // track of already visited indexes
        let visited = new Array(n);
            for(let i=0;i<n;i++)
            {
                visited[i]=new Array(n);
                for(let j=0;j<n;j++)
                {
                    visited[i][j]=false;
                }
            }

        // Flag to indicate whether the
        // path exists or not
        let flag = false;

        for (let i = 0; i < n; i++) {
            for (let j = 0; j < n; j++) {
                // if matrix[i][j] is source
                // and it is not visited
                if (
                    matrix[i][j] == 1
                    && !visited[i][j])

                    // Starting from i, j and
                    // then finding the path
                    if (checkPath(
                            matrix, i, j, visited)) {
                        // if path exists
                        flag = true;
                        break;
                    }
            }
        }
        if (flag)
            document.write("YES<br>");
        else
            document.write("NO<br>");
}

// Method for checking boundaries
function isSafe(i,j,matrix)
{
    if (
            i >= 0 && i < matrix.length
            && j >= 0
            && j < matrix[0].length)
            return true;
        return false;
}

// Returns true if there is a
    // path from a source (a
    // cell with value 1) to a
    // destination (a cell with
    // value 2)
function checkPath(matrix,i,j,visited)
{
    // Checking the boundaries, walls and
        // whether the cell is unvisited
        if (
            isSafe(i, j, matrix)
            && matrix[i][j] != 0
            && !visited[i][j]) {
            // Make the cell visited
            visited[i][j] = true;

            // if the cell is the required
            // destination then return true
            if (matrix[i][j] == 2)
                return true;

            // traverse up
            let up = checkPath(
                matrix, i - 1,
                j, visited);

            // if path is found in up
            // direction return true
            if (up)
                return true;

            // traverse left
            let left
                = checkPath(
                    matrix, i, j - 1, visited);

            // if path is found in left
            // direction return true
            if (left)
                return true;

            // traverse down
            let down = checkPath(
                matrix, i + 1, j, visited);

            // if path is found in down
            // direction return true
            if (down)
                return true;

            // traverse right
            let right
                = checkPath(
                    matrix, i, j + 1,
                    visited);

            // if path is found in right
            // direction return true
            if (right)
                return true;
        }
        // no path has been found
        return false;
}

// driver program to
// check above function
let matrix= [[ 0, 3, 0, 1 ],
             [ 3, 0, 3, 3 ],
             [ 2, 3, 3, 3 ],
             [ 0, 3, 3, 3 ]];

        // calling isPath method
        isPath(matrix, 4);

// This code is contributed by ab2127

</script>

Output

YES

Time Complexity: O(N*M), In the worst case, we have to visit each cell only one time because we keep the visited array for not visiting the already visited cell.
Auxiliary Space: O(N*M), Space is required to store the visited array.

Find whether there is path between two cells in matrix using Breadth First Search:

The idea is to use Breadth-First Search. Consider each cell as a node and each boundary between any two adjacent cells be an edge. so the total number of Node is N * N. So the idea is to do a breadth-first search from the starting cell till the ending cell is found.

Follow the steps below to solve the problem:

• Create an empty Graph having N*N node(Vertex), push all nodes into a graph, and note down the source and sink vertex.
• Now apply BFS on the graph, create a queue and insert the source node in the queue
• Run a loop till the size of the queue is greater than 0
• Remove the front node of the queue and check if the node is the destination if the destination returns true. mark the node
• Check all adjacent cells if unvisited and blank insert them in the queue.
• If the destination is reached return true.

Below is the implementation of the above approach.

C++

// C++ program to find path
// between two cell in matrix
#include <bits/stdc++.h>
using namespace std;
#define N 4

class Graph {
    int V;
    list<int>* adj;

public:
    Graph(int V)
    {
        this->V = V;
        adj = new list<int>[V];
    }
    void addEdge(int s, int d);
    bool BFS(int s, int d);
};

// add edge to graph
void Graph::addEdge(int s, int d) { adj[s].push_back(d); }

// BFS function to find path
// from source to sink
bool Graph::BFS(int s, int d)
{
    // Base case
    if (s == d)
        return true;

    // Mark all the vertices as not visited
    bool* visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    // Create a queue for BFS
    list<int> queue;

    // Mark the current node as visited and
    // enqueue it
    visited[s] = true;
    queue.push_back(s);

    // it will be used to get all adjacent
    // vertices of a vertex
    list<int>::iterator i;

    while (!queue.empty()) {
        // Dequeue a vertex from queue
        s = queue.front();
        queue.pop_front();

        // Get all adjacent vertices of the
        // dequeued vertex s. If a adjacent has
        // not been visited, then mark it visited
        // and enqueue it
        for (i = adj[s].begin(); i != adj[s].end(); ++i) {
            // If this adjacent node is the
            // destination node, then return true
            if (*i == d)
                return true;

            // Else, continue to do BFS
            if (!visited[*i]) {
                visited[*i] = true;
                queue.push_back(*i);
            }
        }
    }

    // If BFS is complete without visiting d
    return false;
}

bool isSafe(int i, int j, int M[][N])
{
    if ((i < 0 || i >= N) || (j < 0 || j >= N)
        || M[i][j] == 0)
        return false;
    return true;
}

// Returns true if there is
// a path from a source (a
// cell with value 1) to a
// destination (a cell with
// value 2)
bool findPath(int M[][N])
{
    // source and destination
    int s, d;
    int V = N * N + 2;
    Graph g(V);

    // create graph with n*n node
    // each cell consider as node
    // Number of current vertex
    int k = 1;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (M[i][j] != 0) {
                // connect all 4 adjacent
                // cell to current cell
                if (isSafe(i, j + 1, M))
                    g.addEdge(k, k + 1);
                if (isSafe(i, j - 1, M))
                    g.addEdge(k, k - 1);
                if (i < N - 1 && isSafe(i + 1, j, M))
                    g.addEdge(k, k + N);
                if (i > 0 && isSafe(i - 1, j, M))
                    g.addEdge(k, k - N);
            }

            // Source index
            if (M[i][j] == 1)
                s = k;

            // Destination index
            if (M[i][j] == 2)
                d = k;
            k++;
        }
    }

    // find path Using BFS
    return g.BFS(s, d);
}

// driver program to check
// above function
int main()
{
    int M[N][N] = { { 0, 3, 0, 1 },
                    { 3, 0, 3, 3 },
                    { 2, 3, 3, 3 },
                    { 0, 3, 3, 3 } };

    (findPath(M) == true) ? cout << "Yes"
                          : cout << "No" << endl;

    return 0;
}

Java

// Java program to find path between two
// cell in matrix
import java.util.*;

class Graph {
    int V;
    List<List<Integer> > adj;

    Graph(int V)
    {
        this.V = V;
        adj = new ArrayList<>(V);
        for (int i = 0; i < V; i++) {
            adj.add(i, new ArrayList<>());
        }
    }

    // add edge to graph
    void addEdge(int s, int d) { adj.get(s).add(d); }

    // BFS function to find path
    // from source to sink
    boolean BFS(int s, int d)
    {
        // Base case
        if (s == d)
            return true;

        // Mark all the vertices as not visited
        boolean[] visited = new boolean[V];

        // Create a queue for BFS
        Queue<Integer> queue = new LinkedList<>();

        // Mark the current node as visited and
        // enqueue it
        visited[s] = true;
        queue.offer(s);

        // it will be used to get all adjacent
        // vertices of a vertex
        List<Integer> edges;

        while (!queue.isEmpty()) {
            // Dequeue a vertex from queue
            s = queue.poll();

            // Get all adjacent vertices of the
            // dequeued vertex s. If a adjacent has
            // not been visited, then mark it visited
            // and enqueue it
            edges = adj.get(s);
            for (int curr : edges) {
                // If this adjacent node is the
                // destination node, then return true
                if (curr == d)
                    return true;

                // Else, continue to do BFS
                if (!visited[curr]) {
                    visited[curr] = true;
                    queue.offer(curr);
                }
            }
        }

        // If BFS is complete without visiting d
        return false;
    }

    static boolean isSafe(int i, int j, int[][] M)
    {
        int N = M.length;
        if ((i < 0 || i >= N) || (j < 0 || j >= N)
            || M[i][j] == 0)
            return false;
        return true;
    }

    // Returns true if there is a
    // path from a source (a
    // cell with value 1) to a
    // destination (a cell with
    // value 2)
    static boolean findPath(int[][] M)
    {
        // Source and destination
        int s = -1, d = -1;
        int N = M.length;
        int V = N * N + 2;
        Graph g = new Graph(V);

        // Create graph with n*n node
        // each cell consider as node
        int k = 1; // Number of current vertex
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if (M[i][j] != 0) {

                    // connect all 4 adjacent
                    // cell to current cell
                    if (isSafe(i, j + 1, M))
                        g.addEdge(k, k + 1);
                    if (isSafe(i, j - 1, M))
                        g.addEdge(k, k - 1);
                    if (i < N - 1 && isSafe(i + 1, j, M))
                        g.addEdge(k, k + N);
                    if (i > 0 && isSafe(i - 1, j, M))
                        g.addEdge(k, k - N);
                }

                // source index
                if (M[i][j] == 1)
                    s = k;

                // destination index
                if (M[i][j] == 2)
                    d = k;
                k++;
            }
        }

        // find path Using BFS
        return g.BFS(s, d);
    }

    // Driver program to check above function
    public static void main(String[] args) throws Exception
    {
        int[][] M = { { 0, 3, 0, 1 },
                      { 3, 0, 3, 3 },
                      { 2, 3, 3, 3 },
                      { 0, 3, 3, 3 } };

        System.out.println(((findPath(M)) ? "Yes" : "No"));
    }
}

// This code is contributed by abhay379201

Python3

# Python3 program to find path between two
# cell in matrix
from collections import defaultdict


class Graph:
    def __init__(self):
        self.graph = defaultdict(list)

    # add edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)

    # BFS function to find path from source to sink
    def BFS(self, s, d):

        # Base case
        if s == d:
            return True

        # Mark all the vertices as not visited
        visited = [False]*(len(self.graph) + 1)

        # Create a queue for BFS
        queue = []
        queue.append(s)

        # Mark the current node as visited and
        # enqueue it
        visited[s] = True
        while(queue):

            # Dequeue a vertex from queue
            s = queue.pop(0)

            # Get all adjacent vertices of the
            # dequeued vertex s. If a adjacent has
            # not been visited, then mark it visited
            # and enqueue it
            for i in self.graph[s]:

                # If this adjacent node is the destination
                # node, then return true
                if i == d:
                    return True

                # Else, continue to do BFS
                if visited[i] == False:
                    queue.append(i)
                    visited[i] = True

        # If BFS is complete without visiting d
        return False


def isSafe(i, j, matrix):
    if i >= 0 and i <= len(matrix) and j >= 0 and j <= len(matrix[0]):
        return True
    else:
        return False

# Returns true if there is a path from a source (a
# cell with value 1) to a destination (a cell with
# value 2)


def findPath(M):
    s, d = None, None  # source and destination
    N = len(M)
    g = Graph()

    # create graph with n * n node
    # each cell consider as node
    k = 1  # Number of current vertex
    for i in range(N):
        for j in range(N):
            if (M[i][j] != 0):

                # connect all 4 adjacent cell to
                # current cell
                if (isSafe(i, j + 1, M)):
                    g.addEdge(k, k + 1)
                if (isSafe(i, j - 1, M)):
                    g.addEdge(k, k - 1)
                if (isSafe(i + 1, j, M)):
                    g.addEdge(k, k + N)
                if (isSafe(i - 1, j, M)):
                    g.addEdge(k, k - N)

            if (M[i][j] == 1):
                s = k

            # destination index
            if (M[i][j] == 2):
                d = k
            k += 1

    # find path Using BFS
    return g.BFS(s, d)


# Driver code
if __name__ == '__main__':
    M = [[0, 3, 0, 1], [3, 0, 3, 3], [2, 3, 3, 3], [0, 3, 3, 3]]
    if findPath(M):
        print("Yes")
    else:
        print("No")

# This Code is Contributed by Vikash Kumar 37

C#

// C# program to find path between two
// cell in matrix
using System;
using System.Collections.Generic;

class Graph {
  public int V;
  public List<List<int> > adj;

  public Graph(int V)
  {
    this.V = V;
    adj = new List<List<int>>();
    for (int i = 0; i < V; i++) {
      adj.Add(new List<int>());
    }
  }

  // Add edge to graph
  public void AddEdge(int s, int d) { adj[s].Add(d); }

  // BFS function to find path
  // from source to sink
  public bool BFS(int s, int d)
  {
    // Base case
    if (s == d)
      return true;

    // Mark all the vertices as not visited
    bool[] visited = new bool[V];

    // Create a queue for BFS
    List<int> queue = new List<int>();

    // Mark the current node as visited and
    // enqueue it
    visited[s] = true;
    queue.Add(s);

    // it will be used to get all adjacent
    // vertices of a vertex
    List<int> edges = new List<int>();

    while (queue.Count != 0 ) {
      // Dequeue a vertex from queue
      s = queue[0];
      queue.RemoveAt(0);

      // Get all adjacent vertices of the
      // dequeued vertex s. If a adjacent has
      // not been visited, then mark it visited
      // and enqueue it
      edges = adj[s];
      foreach (int curr in edges) {
        // If this adjacent node is the
        // destination node, then return true
        if (curr == d)
          return true;

        // Else, continue to do BFS
        if (!visited[curr]) {
          visited[curr] = true;
          queue.Add(curr);
        }
      }
    }

    // If BFS is complete without visiting d
    return false;
  }

  static bool isSafe(int i, int j, int[, ] M)
  {

    if ((i < 0 || i >= M.GetLength(0)) || (j < 0 || j >= M.GetLength(1))
        || M[i, j] == 0)
      return false;
    return true;
  }

  // Returns true if there is a
  // path from a source (a
  // cell with value 1) to a
  // destination (a cell with
  // value 2)
  static bool findPath(int[, ] M)
  {
    // Source and destination
    int s = -1, d = -1;
    int N = M.GetLength(0);
    int V = N * N + 2;
    Graph g = new Graph(V);

    // Create graph with n*n node
    // each cell consider as node
    int k = 1; // Number of current vertex
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
        if (M[i, j] != 0) {

          // connect all 4 adjacent
          // cell to current cell
          if (isSafe(i, j + 1, M))
            g.AddEdge(k, k + 1);
          if (isSafe(i, j - 1, M))
            g.AddEdge(k, k - 1);
          if (i < N - 1 && isSafe(i + 1, j, M))
            g.AddEdge(k, k + N);
          if (i > 0 && isSafe(i - 1, j, M))
            g.AddEdge(k, k - N);
        }

        // source index
        if (M[i, j] == 1)
          s = k;

        // destination index
        if (M[i, j] == 2)
          d = k;
        k++;
      }
    }

    // find path Using BFS
    return g.BFS(s, d);
  }

  // Driver program to check above function
  public static void Main(string[] args)
  {
    int[, ] M = { { 0, 3, 0, 1 },
                 { 3, 0, 3, 3 },
                 { 2, 3, 3, 3 },
                 { 0, 3, 3, 3 } };

    Console.WriteLine(((findPath(M)) ? "Yes" : "No"));
  }
}

// This code is contributed by phasing17

Javascript

<script>

// JavaScript program to find path between two
// cell in matrix

let V;
let adj=[];

function Graph(v)
{
    V=v;
    for (let i = 0; i < V; i++)
    {
        adj.push([]);
    }
}

// add edge to graph
function addEdge(s,d)
{
    adj[s].push(d);
}

// BFS function to find path
    // from source to sink
function  BFS(s,d)
{
    // Base case
        if (s == d)
            return true;

        // Mark all the vertices as not visited
        let visited = new Array(V);
        for(let i=0;i<V;i++)
        {
            visited[i]=false;
        }

        // Create a queue for BFS
        let queue=[];

        // Mark the current node as visited and
        // enqueue it
        visited[s] = true;
        queue.push(s);

        // it will be used to get all adjacent
        // vertices of a vertex
        let edges;

        while (queue.length!=0) {
            // Dequeue a vertex from queue
            s = queue.shift();

            // Get all adjacent vertices of the
            // dequeued vertex s. If a adjacent has
            // not been visited, then mark it visited
            // and enqueue it
            edges = adj[s];
            for (let curr=0;curr< edges.length;curr++) {
                // If this adjacent node is the
                // destination node, then return true
                if (edges[curr] == d)
                    return true;

                // Else, continue to do BFS
                if (!visited[edges[curr]]) {
                    visited[edges[curr]] = true;
                    queue.push(edges[curr]);
                }
            }
        }

        // If BFS is complete without visiting d
        return false;
}

function isSafe(i,j,M)
{
    let N = M.length;
        if (
            (i < 0 || i >= N)
            || (j < 0 || j >= N)
            || M[i][j] == 0)
            return false;
        return true;
}

// Returns true if there is a
    // path from a source (a
    // cell with value 1) to a
    // destination (a cell with
    // value 2)
function findPath(M)
{
    // Source and destination
        let s = -1, d = -1;
        let N = M.length;
        let V = N * N + 2;
        Graph(V);

        // Create graph with n*n node
        // each cell consider as node
        let k = 1; // Number of current vertex
        for (let i = 0; i < N; i++) {
            for (let j = 0; j < N; j++) {
                if (M[i][j] != 0) {

                    // connect all 4 adjacent
                    // cell to current cell
                    if (isSafe(i, j + 1, M))
                        addEdge(k, k + 1);
                    if (isSafe(i, j - 1, M))
                        addEdge(k, k - 1);
                    if (i < N - 1
                        && isSafe(i + 1, j, M))
                        addEdge(k, k + N);
                    if (i > 0 && isSafe(i - 1, j, M))
                        addEdge(k, k - N);
                }

                // source index
                if (M[i][j] == 1)
                    s = k;

                // destination index
                if (M[i][j] == 2)
                    d = k;
                k++;
            }
        }

        // find path Using BFS
        return BFS(s, d);
}

 // Driver program to check above function
let M = [[ 0, 3, 0, 1 ],
                      [ 3, 0, 3, 3 ],
                      [ 2, 3, 3, 3 ],
                      [ 0, 3, 3, 3 ]];
document.write(((findPath(M)) ? "Yes" : "No"));


// This code is contributed by patel2127

</script>

Output

Yes

Time Complexity: O(N*M), Every cell of the matrix is visited only once so the time complexity is O(N*M).
Auxiliary Space: O(N*M), Space is required to store the visited array and to create the queue.

Find whether there is path between two cells in matrix using Breadth First Search (On matrix):

The idea is to use Breadth-First Search on the matrix itself. Consider a cell=(i,j) as a vertex v in the BFS queue. A new vertex u is placed in the BFS queue if u=(i+1,j) or u=(i-1,j) or u=(i,j+1) or u=(i,j-1). Starting the BFS algorithm from cell=(i,j) such that M[i][j] is 1 and stopping either if there was a reachable vertex u=(i,j) such that M[i][j] is 2 and returning true or every cell was covered and there was no such a cell and returning false.

Follow the steps below to solve the problem:

• Create BFS queue q
• scan the matrix, if there exists a cell in the matrix such that its value is 1 then push it to q
• Run BFS algorithm with q, skipping cells that are not valid. i.e: they are walls (value is 0) or outside the matrix bounds and marking them as walls upon successful visitation.
  • If in the BFS algorithm process there was a vertex x=(i,j) such that M[i][j] is 2 stop and return true.
• BFS algorithm terminated without returning true then there was no element M[i][j] which is 2, then return false

Below is the implementation of the above approach:

C++

#include <iostream>
#include <queue>
using namespace std;
#define R 4
#define C 4

// Structure to define a vertex u=(i,j)
typedef struct BFSElement {
    BFSElement(int i, int j)
    {
        this->i = i;
        this->j = j;
    }
    int i;
    int j;
} BFSElement;

bool findPath(int M[R][C])
{
    // 1) Create BFS queue q
    queue<BFSElement> q;

    // 2)scan the matrix
    for (int i = 0; i < R; ++i) {
        for (int j = 0; j < C; ++j) {

            // if there exists a cell in the matrix such
            // that its value is 1 then push it to q
            if (M[i][j] == 1) {
                q.push(BFSElement(i, j));
                break;
            }
        }
    }

    // 3) run BFS algorithm with q.
    while (!q.empty()) {
        BFSElement x = q.front();
        q.pop();
        int i = x.i;
        int j = x.j;

        // skipping cells which are not valid.
        // if outside the matrix bounds
        if (i >= 0 && i < R && j >= 0 && j < C)
        {

        // if they are walls (value is 0).
        if (M[i][j] == 0)
            continue;

        // 3.1) if in the BFS algorithm process there was a
        // vertex x=(i,j) such that M[i][j] is 2 stop and
        // return true
        if (M[i][j] == 2)
            return true;

        // marking as wall upon successful visitation
        M[i][j] = 0;

        // pushing to queue u=(i,j+1),u=(i,j-1)
        //                 u=(i+1,j),u=(i-1,j)
        for (int k = -1; k <= 1; k += 2) {
            q.push(BFSElement(i + k, j));
            q.push(BFSElement(i, j + k));
        }
        }
    }

    // BFS algorithm terminated without returning true
    // then there was no element M[i][j] which is 2, then
    // return false
    return false;
}

// Main Driver code
int main()
{

    int M[R][C] = { { 0, 3, 0, 1 },
                    { 3, 0, 3, 3 },
                    { 2, 3, 3, 3 },
                    { 0, 3, 3, 3 } };

    (findPath(M) == true) ? cout << "Yes"
                          : cout << "No" << endl;

    return 0;
}

Java

import java.io.*;
import java.util.*;

class BFSElement {
    int i, j;
    BFSElement(int i, int j)
    {
        this.i = i;
        this.j = j;
    }
}

class GFG {
    static int R = 4, C = 4;
    BFSElement b;

    static boolean findPath(int M[][])
    {

        // 1) Create BFS queue q
        Queue<BFSElement> q = new LinkedList<>();

        // 2)scan the matrix
        for (int i = 0; i < R; ++i) {
            for (int j = 0; j < C; ++j) {

                // if there exists a cell in the matrix such
                // that its value is 1 then push it to q
                if (M[i][j] == 1) {
                    q.add(new BFSElement(i, j));
                    break;
                }
            }
        }

        // 3) run BFS algorithm with q.
        while (q.size() != 0) {
            BFSElement x = q.peek();
            q.remove();
            int i = x.i;
            int j = x.j;

            // skipping cells which are not valid.
            // if outside the matrix bounds
            if (i < 0 || i >= R || j < 0 || j >= C)
                continue;

            // if they are walls (value is 0).
            if (M[i][j] == 0)
                continue;

            // 3.1) if in the BFS algorithm process there
            // was a vertex x=(i,j) such that M[i][j] is 2
            // stop and return true
            if (M[i][j] == 2)
                return true;

            // marking as wall upon successful visitation
            M[i][j] = 0;

            // pushing to queue u=(i,j+1),u=(i,j-1)
            // u=(i+1,j),u=(i-1,j)
            for (int k = -1; k <= 1; k += 2) {
                q.add(new BFSElement(i + k, j));
                q.add(new BFSElement(i, j + k));
            }
        }

        // BFS algorithm terminated without returning true
        // then there was no element M[i][j] which is 2,
        // then return false
        return false;
    }

    // Main Driver code
    public static void main(String[] args)
    {
        int M[][] = { { 0, 3, 0, 1 },
                      { 3, 0, 3, 3 },
                      { 2, 3, 3, 3 },
                      { 0, 3, 3, 3 } };

        if (findPath(M) == true)
            System.out.println("Yes");
        else
            System.out.println("No");
    }
}

// This code is contributed by avanitrachhadiya2155

Python3

class BFSElement:
    def __init__(self, i, j):
        self.i = i
        self.j = j


R, C = 4, 4


def findPath(M):

    # 1) Create BFS queue q
    q = []

    # 2)scan the matrix
    for i in range(R):
        for j in range(C):

            # if there exists a cell in the matrix such
            # that its value is 1 then append it to q
            if (M[i][j] == 1):
                q.append(BFSElement(i, j))
                break

    # 3) run BFS algorithm with q.
    while (len(q) != 0):
        x = q[0]
        q = q[1:]

        i = x.i
        j = x.j

        # skipping cells which are not valid.
        # if outside the matrix bounds
        if (i < 0 or i >= R or j < 0 or j >= C):
            continue

        # if they are walls (value is 0).
        if (M[i][j] == 0):
            continue

        # 3.1) if in the BFS algorithm process there was a
        # vertex x=(i,j) such that M[i][j] is 2 stop and
        # return True
        if (M[i][j] == 2):
            return True

        # marking as wall upon successful visitation
        M[i][j] = 0

        # appending to queue u=(i,j+1),u=(i,j-1)
        # u=(i+1,j),u=(i-1,j)
        for k in range(-1, 2, 2):
            q.append(BFSElement(i + k, j))
            q.append(BFSElement(i, j + k))

    # BFS algorithm terminated without returning True
    # then there was no element M[i][j] which is 2, then
    # return false
    return False


# Main Driver code
M = [[0, 3, 0, 1],
     [3, 0, 3, 3],
     [2, 3, 3, 3],
     [0, 3, 3, 3]]
if(findPath(M) == True):
    print("Yes")
else:
    print("No")

# This code is contributed by shinjanpatra

C#

using System;
using System.Collections.Generic;

public class BFSElement {
    public int i, j;
    public BFSElement(int i, int j)
    {
        this.i = i;
        this.j = j;
    }
}

public class GFG {
    static int R = 4, C = 4;
    static bool findPath(int[, ] M)
    {

        // 1) Create BFS queue q
        Queue<BFSElement> q = new Queue<BFSElement>();

        // 2)scan the matrix
        for (int i = 0; i < R; ++i) {
            for (int j = 0; j < C; ++j) {

                // if there exists a cell in the matrix such
                // that its value is 1 then push it to q
                if (M[i, j] == 1) {
                    q.Enqueue(new BFSElement(i, j));
                    break;
                }
            }
        }

        // 3) run BFS algorithm with q.
        while (q.Count != 0) {
            BFSElement x = q.Peek();
            q.Dequeue();
            int i = x.i;
            int j = x.j;

            // skipping cells which are not valid.
            // if outside the matrix bounds
            if (i < 0 || i >= R || j < 0 || j >= C)
                continue;

            // if they are walls (value is 0).
            if (M[i, j] == 0)
                continue;

            // 3.1) if in the BFS algorithm process there
            // was a vertex x=(i,j) such that M[i][j] is 2
            // stop and return true
            if (M[i, j] == 2)
                return true;

            // marking as wall upon successful visitation
            M[i, j] = 0;

            // pushing to queue u=(i,j+1),u=(i,j-1)
            // u=(i+1,j),u=(i-1,j)
            for (int k = -1; k <= 1; k += 2) {
                q.Enqueue(new BFSElement(i + k, j));
                q.Enqueue(new BFSElement(i, j + k));
            }
        }

        // BFS algorithm terminated without returning true
        // then there was no element M[i][j] which is 2,
        // then return false
        return false;
    }

    // Main Driver code
    static public void Main()
    {
        int[, ] M = { { 0, 3, 0, 1 },
                      { 3, 0, 3, 3 },
                      { 2, 3, 3, 3 },
                      { 0, 3, 3, 3 } };

        if (findPath(M) == true)
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
}

// This code is contributed by rag2127

Javascript

<script>

class BFSElement
{
    constructor(i,j)
    {
        this.i=i;
        this.j=j;
    }
}

let R = 4, C = 4;
let  b;

function findPath(M)
{
    // 1) Create BFS queue q
        let q = [];

    // 2)scan the matrix
        for (let i = 0; i < R; ++i)
        {
            for (let j = 0; j < C; ++j)
            {

                // if there exists a cell in the matrix such
                // that its value is 1 then push it to q
                if (M[i][j] == 1) {
                    q.push(new BFSElement(i, j));
                    break;
                }
            }

        }

    // 3) run BFS algorithm with q.
        while (q.length != 0)
        {
            let x = q.shift();

            let i = x.i;
            let j = x.j;

            // skipping cells which are not valid.
            // if outside the matrix bounds
            if (i < 0 || i >= R || j < 0 || j >= C)
                continue;

            // if they are walls (value is 0).
            if (M[i][j] == 0)
                continue;

            // 3.1) if in the BFS algorithm process there was a
            // vertex x=(i,j) such that M[i][j] is 2 stop and
            // return true
            if (M[i][j] == 2)
                return true;

            // marking as wall upon successful visitation
            M[i][j] = 0;

            // pushing to queue u=(i,j+1),u=(i,j-1)
            // u=(i+1,j),u=(i-1,j)
            for (let k = -1; k <= 1; k += 2)
            {
                q.push(new BFSElement(i + k, j));
                q.push(new BFSElement(i, j + k));
            }
        }

    // BFS algorithm terminated without returning true
    // then there was no element M[i][j] which is 2, then
    // return false
        return false;
}

// Main Driver code
let M=[[ 0, 3, 0, 1 ],
                    [ 3, 0, 3, 3 ],
                    [ 2, 3, 3, 3 ],
                    [ 0, 3, 3, 3 ]];
if(findPath(M) == true)
    document.write("Yes");
else
    document.write("No");


// This code is contributed by unknown2108
</script>

Output

Yes

Time Complexity: O(N*M), Every cell of the matrix is visited only once so the time complexity is O(N*M).
Auxiliary Space: O(N*M), Space is required to store the visited array and to create the queue.