Find two numbers whose sum and GCD are given

Given sum and gcd of two numbers 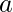and 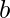. The task is to find both the numbers a and b. If the numbers do not exist then print .
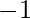Examples:

Input: sum = 6, gcd = 2 
Output: a = 4, b = 2 
4 + 2 = 6 and GCD(4, 2) = 2
Input: sum = 7, gcd = 2 
Output: -1 
There are no such numbers whose sum is 7 and GCD is 2 

Approach: As GCD is given then it is known that both the numbers will be multiples of it. 

• Choose the first number as gcd then the other number will be sum – gcd.
• If the sum of both the numbers chosen in the previous step equals to sum then print both the numbers.
• Else the numbers do not exist and print -1 instead.

Below is the implementation of the above approach: 

C++

// C++ program to find two numbers
// whose sum and GCD is given
#include <bits/stdc++.h>
using namespace std;

// Function to find two numbers
// whose sum and gcd is given
void findTwoNumbers(int sum, int gcd)
{
    // sum != gcd checks that both the
    // numbers are positive or not
    if (__gcd(gcd, sum - gcd) == gcd && sum != gcd)
        cout << "a = " << min(gcd, sum - gcd)
             << ", b = " << sum - min(gcd, sum - gcd)
             << endl;
    else
        cout << -1 << endl;
}

// Driver code
int main()
{
    int sum = 8;
    int gcd = 2;

    findTwoNumbers(sum, gcd);

    return 0;
}

Java

// Java program to find two numbers
// whose sum and GCD is given
import java.util.*;
class Solution{

//function to find gcd of two numbers
static int __gcd(int a,int b)
{
    if (b==0) return a;
   return __gcd(b,a%b);
}

// Function to find two numbers
// whose sum and gcd is given
static void findTwoNumbers(int sum, int gcd)
{
    // sum != gcd checks that both the
    // numbers are positive or not
    if (__gcd(gcd, sum - gcd) == gcd && sum != gcd)
        System.out.println(  "a = " + Math.min(gcd, sum - gcd)
            + ", b = " + (int)(sum - Math.min(gcd, sum - gcd)) );
    else
        System.out.println( -1 );
}

// Driver code
public static void main(String args[])
{
    int sum = 8;
    int gcd = 2;

    findTwoNumbers(sum, gcd);

}


}
//contributed by Arnab Kundu

Python3

# Python 3 program to find two numbers
# whose sum and GCD is given
from math import gcd as __gcd

# Function to find two numbers
# whose sum and gcd is given
def findTwoNumbers(sum, gcd):

    # sum != gcd checks that both the
    # numbers are positive or not
    if (__gcd(gcd, sum - gcd) == gcd and
                          sum != gcd):
        print("a =", min(gcd, sum - gcd),
              ", b =", sum - min(gcd, sum - gcd))
    else:
        print(-1)

# Driver code
if __name__ == '__main__':
    sum = 8
    gcd = 2

    findTwoNumbers(sum, gcd)

# This code is contributed by
# Surendra_Gangwar

C#

// C# program to find two numbers
// whose sum and GCD is given
using System;
class GFG
{

// function to find gcd of two numbers
static int __gcd(int a, int b)
{
    if (b == 0)
        return a;
    return __gcd(b, a % b);
}

// Function to find two numbers
// whose sum and gcd is given
static void findTwoNumbers(int sum, int gcd)
{
    // sum != gcd checks that both the
    // numbers are positive or not
    if (__gcd(gcd, sum - gcd) == gcd && sum != gcd)
        Console.WriteLine("a = " + Math.Min(gcd, sum - gcd) +
            ", b = " + (int)(sum - Math.Min(gcd, sum - gcd)));
    else
        Console.WriteLine( -1 );
}

// Driver code
public static void Main()
{
    int sum = 8;
    int gcd = 2;

    findTwoNumbers(sum, gcd);
}
}

// This code is contributed by anuj_67..

PHP

<?php
// PHP program to find two numbers
// whose sum and GCD is given

// Function to find gcd of two numbers
function __gcd($a, $b)
{
    if ($b == 0)
        return $a;

    return __gcd($b, $a % $b);
}

// Function to find two numbers
// whose sum and gcd is given
function findTwoNumbers($sum, $gcd)
{
    // sum != gcd checks that both the
    // numbers are positive or not
    if (__gcd($gcd, $sum - $gcd) == $gcd &&
                            $sum != $gcd)
        echo "a = " , min($gcd, $sum - $gcd),
             " b = ", (int)($sum - min($gcd,
                            $sum - $gcd));
    else
        echo (-1);
}

// Driver code
$sum = 8;
$gcd = 2;

findTwoNumbers($sum, $gcd);

// This code is contributed by Sachin
?>

Javascript

<script>

// Javascript program to find two numbers
// whose sum and GCD is given

//function to find gcd of two numbers
function __gcd(a, b)
{
    if (b==0) return a;
   return __gcd(b,a%b);
}

// Function to find two numbers
// whose sum and gcd is given
function findTwoNumbers(sum, gcd)
{
    // sum != gcd checks that both the
    // numbers are positive or not
    if (__gcd(gcd, sum - gcd) == gcd && sum != gcd)
        document.write(  "a = " + Math.min(gcd, sum - gcd)
            + ", b = " + (sum - Math.min(gcd, sum - gcd)) );
    else
        document.write( -1 );
}

// Driver code

    let sum = 8;
    let gcd = 2;

    findTwoNumbers(sum, gcd);

</script>

Output:

a = 2, b = 6

Time Complexity: O(log(min(a, b))), where a and b are two parameters of gcd.

Auxiliary Space: O(log(min(a, b)))