Find two integers X and Y with given GCD P and given difference between their squares Q

Given two integers P and Q, the task is to find any two integers whose Greatest Common Divisor(GCD) is P and the difference between their squares is Q. If there doesn’t exist any such integers, then print “-1”.

Examples: 

Input: P = 3, Q = 27
Output:  6 3
Explanation:
Consider the two number as 6, 3. Now, the GCD(6, 3) = 3 and 6*6 – 3*3 = 27 which satisfies the condition.

Input: P = 1, Q = 100
Output: -1

Approach: The given problem can be solved using based on the following observations:

The given equation can also be written as:  

=> 
=> 

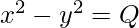
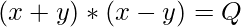
Now for an integral solution of the given equation:  

(x+y)(x-y)  is always an integer 
=> (x+y)(x-y)  are divisors of Q

Let  (x + y) = p1 and (x + y) = p2 
be the two equations where p1 & p2 are the divisors of Q
such that p1 * p2 = Q.

Solving for the above two equation we have:  

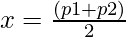=> and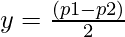   

From the above calculations, for x and y to be integral, then the sum of divisors must be even. Since there are 4 possible values for two values of x and y as (+x, +y), (+x, -y), (-x, +y) and (-x, -y). 
Therefore the total number of possible solution is given by 4*(count pairs of divisors with even sum).

Now among these pairs, find the pair with GCD as P and print the pair. If no such pair exists, print -1.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to print a valid pair with
// the given criteria
int printValidPair(int P, int Q)
{

    // Iterate over the divisors of Q
    for (int i = 1; i * i <= Q; i++) {

        // check if Q is a multiple of i
        if (Q % i == 0) {

            // L = (A - B) <- 1st equation
            // R = (A + B) <- 2nd equation
            int L = i;
            int R = Q / i;

            // Calculate value of A
            int A = (L + R) / 2;

            // Calculate value of B
            int B = (R - L) / 2;

            // As A and B both are integers
            // so the parity of L and R
            // should be the same
            if (L % 2 != R % 2) {
                continue;
            }

            // Check the first condition
            if (__gcd(A, B) == P) {
                cout << A << " " << B;
                return 0;
            }
        }
    }

    // If no such A, B exist
    cout << -1;

    return 0;
}

// Driver Code
int main()
{
    int P = 3, Q = 27;
    printValidPair(P, Q);

    return 0;
}

Java

// Java program for the above approach
import java.util.*;

class GFG{

// Function to print a valid pair with
// the given criteria
static int printValidPair(int P, int Q)
{

    // Iterate over the divisors of Q
    for (int i = 1; i * i <= Q; i++) {

        // check if Q is a multiple of i
        if (Q % i == 0) {

            // L = (A - B) <- 1st equation
            // R = (A + B) <- 2nd equation
            int L = i;
            int R = Q / i;

            // Calculate value of A
            int A = (L + R) / 2;

            // Calculate value of B
            int B = (R - L) / 2;

            // As A and B both are integers
            // so the parity of L and R
            // should be the same
            if (L % 2 != R % 2) {
                continue;
            }

            // Check the first condition
            if (__gcd(A, B) == P) {
                System.out.print(A+ " " +  B);
                return 0;
            }
        }
    }

    // If no such A, B exist
    System.out.print(-1);
    return 0;

}
static int __gcd(int a, int b)
{
    return b == 0? a:__gcd(b, a % b);
}

// Driver Code
public static void main(String[] args)
{
    int P = 3, Q = 27;
    printValidPair(P, Q);
}
}

// This code is contributed by 29AjayKumar

Python3

# python program for the above approach
import math

# Function to print a valid pair with
# the given criteria
def printValidPair(P, Q):

    # Iterate over the divisors of Q
    for i in range(1, int(math.sqrt(Q)) + 1):

        # check if Q is a multiple of i
        if (Q % i == 0):

            # L = (A - B) <- 1st equation
            # R = (A + B) <- 2nd equation
            L = i
            R = Q // i

            # Calculate value of A
            A = (L + R) // 2

            # Calculate value of B
            B = (R - L) // 2

            # As A and B both are integers
            # so the parity of L and R
            # should be the same
            if (L % 2 != R % 2):
                continue

            # Check the first condition
            if (math.gcd(A, B) == P):
                print(f"{A} {B}")
                return 0

    # If no such A, B exist
    print(-1)

    return 0

# Driver Code
if __name__ == "__main__":

    P = 3
    Q = 27
    printValidPair(P, Q)

    # This code is contributed by rakeshsahni

C#

// C# program for the above approach
using System;
class GFG
{

    // Function to print a valid pair with
    // the given criteria
    static int printValidPair(int P, int Q)
    {

        // Iterate over the divisors of Q
        for (int i = 1; i * i <= Q; i++)
        {

            // check if Q is a multiple of i
            if (Q % i == 0)
            {

                // L = (A - B) <- 1st equation
                // R = (A + B) <- 2nd equation
                int L = i;
                int R = Q / i;

                // Calculate value of A
                int A = (L + R) / 2;

                // Calculate value of B
                int B = (R - L) / 2;

                // As A and B both are integers
                // so the parity of L and R
                // should be the same
                if (L % 2 != R % 2)
                {
                    continue;
                }

                // Check the first condition
                if (__gcd(A, B) == P)
                {
                    Console.Write(A + " " + B);
                    return 0;
                }
            }
        }

        // If no such A, B exist
        Console.Write(-1);
        return 0;

    }
    static int __gcd(int a, int b)
    {
        return b == 0 ? a : __gcd(b, a % b);
    }

    // Driver Code
    public static void Main()
    {
        int P = 3, Q = 27;
        printValidPair(P, Q);
    }
}

// This code is contributed by gfgking

Javascript

<script>
       // JavaScript code for the above approach
       // Recursive function to return gcd of a and b
       function __gcd(a, b) {
           // Everything divides 0
           if (a == 0)
               return b;
           if (b == 0)
               return a;

           // base case
           if (a == b)
               return a;

           // a is greater
           if (a > b)
               return __gcd(a - b, b);
           return __gcd(a, b - a);
       }

       // Function to print a valid pair with
       // the given criteria
       function printValidPair(P, Q) {

           // Iterate over the divisors of Q
           for (let i = 1; i * i <= Q; i++) {

               // check if Q is a multiple of i
               if (Q % i == 0) {

                   // L = (A - B) <- 1st equation
                   // R = (A + B) <- 2nd equation
                   let L = i;
                   let R = Q / i;

                   // Calculate value of A
                   let A = (L + R) / 2;

                   // Calculate value of B
                   let B = (R - L) / 2;

                   // As A and B both are integers
                   // so the parity of L and R
                   // should be the same
                   if (L % 2 != R % 2) {
                       continue;
                   }

                   // Check the first condition
                   if (__gcd(A, B) == P) {
                       document.write(A + " " + B);
                       return 0;
                   }
               }
           }

           // If no such A, B exist
           document.write(-1);

           return 0;
       }

       // Driver Code
       let P = 3, Q = 27;
       printValidPair(P, Q);

 // This code is contributed by Potta Lokesh
   </script>

Output:

6 3

Time Complexity: O(sqrt(Q))
Auxiliary Space: O(1)