Find two disjoint good sets of vertices in a given graph
Last Updated :
05 Oct, 2021
Given an undirected unweighted graph with N vertices and M edges. The task is to find two disjoint good sets of vertices. A set X is called good if for every edge UV in the graph at least one of the endpoint belongs to X(i.e, U or V or both U and V belong to X).
If it is not possible to make such sets then print -1.
Examples:
Input :
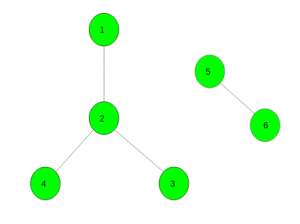
Output : {1 3 4 5} ,{2 6}
One disjoint good set contains vertices {1, 3, 4, 5} and other contains {2, 6}.
Input :
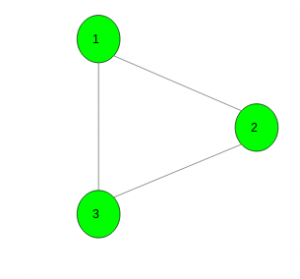
Output : -1
Approach:
One of the observations is that there is no edge UV that U and V are in the same set. The two good sets form a bipartition of the graph, so the graph has to be bipartite. And being bipartite is also sufficient. Read about bipartition here.
Below is the implementation of the above approach :
C++
#include <bits/stdc++.h>
using namespace std;
#define N 100005
vector<int> gr[N], dis[2];
bool vis[N];
int colour[N];
bool bip;
void Add_edge(int x, int y)
{
gr[x].push_back(y);
gr[y].push_back(x);
}
void dfs(int x, int col)
{
vis[x] = true;
colour[x] = col;
for (auto i : gr[x]) {
if (!vis[i])
dfs(i, col ^ 1);
else if (colour[i] == col)
bip = false;
}
}
void goodsets(int n)
{
bip = true;
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
if (!bip)
cout << -1;
else {
for (int i = 1; i <= n; i++)
dis[colour[i]].push_back(i);
for (int i = 0; i < 2; i++) {
for (int j = 0; j < dis[i].size(); j++)
cout << dis[i][j] << " ";
cout << endl;
}
}
}
int main()
{
int n = 6, m = 4;
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(2, 4);
Add_edge(5, 6);
goodsets(n);
}
|
Java
import java.util.*;
class GFG
{
static int N = 100005;
@SuppressWarnings("unchecked")
static Vector<Integer>[] gr = new Vector[N],
dis = new Vector[2];
static
{
for (int i = 0; i < N; i++)
gr[i] = new Vector<>();
for (int i = 0; i < 2; i++)
dis[i] = new Vector<>();
}
static boolean[] vis = new boolean[N];
static int[] color = new int[N];
static boolean bip;
static void add_edge(int x, int y)
{
gr[x].add(y);
gr[y].add(x);
}
static void dfs(int x, int col)
{
vis[x] = true;
color[x] = col;
for (int i : gr[x])
{
if (!vis[i])
dfs(i, col ^ 1);
else if (color[i] == col)
bip = false;
}
}
static void goodsets(int n)
{
bip = true;
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
if (!bip)
System.out.println(-1);
else
{
for (int i = 1; i <= n; i++)
dis[color[i]].add(i);
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < dis[i].size(); j++)
System.out.print(dis[i].elementAt(j) + " ");
System.out.println();
}
}
}
public static void main(String[] args)
{
int n = 6, m = 4;
add_edge(1, 2);
add_edge(2, 3);
add_edge(2, 4);
add_edge(5, 6);
goodsets(n);
}
}
|
Python3
N = 100005
gr = [[] for i in range(N)]
dis = [[] for i in range(2)]
vis = [False for i in range(N)]
colour = [0 for i in range(N)]
bip = 0
def Add_edge(x, y):
gr[x].append(y)
gr[y].append(x)
def dfs(x, col):
vis[x] = True
colour[x] = col
for i in gr[x]:
if (vis[i] == False):
dfs(i, col ^ 1)
elif (colour[i] == col):
bip = False
def goodsets(n):
bip = True
for i in range(1, n + 1, 1):
if (vis[i] == False):
dfs(i, 0)
if (bip == 0):
print(-1)
else:
for i in range(1, n + 1, 1):
dis[colour[i]].append(i)
for i in range(2):
for j in range(len(dis[i])):
print(dis[i][j], end = " ")
print('\n', end = "")
if __name__ == '__main__':
n = 6
m = 4
Add_edge(1, 2)
Add_edge(2, 3)
Add_edge(2, 4)
Add_edge(5, 6)
goodsets(n)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int N = 100005;
static List<int>[] gr =
new List<int>[N],
dis = new List<int>[2];
static bool[] vis = new bool[N];
static int[] color = new int[N];
static bool bip;
static void add_edge(int x,
int y)
{
gr[x].Add(y);
gr[y].Add(x);
}
static void dfs(int x,
int col)
{
vis[x] = true;
color[x] = col;
foreach (int i in gr[x])
{
if (!vis[i])
dfs(i, col ^ 1);
else if (color[i] == col)
bip = false;
}
}
static void goodsets(int n)
{
bip = true;
for (int i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
if (!bip)
Console.WriteLine(-1);
else
{
for (int i = 1;
i <= n; i++)
dis[color[i]].Add(i);
for (int i = 0; i < 2; i++)
{
for (int j = 0;
j < dis[i].Count; j++)
Console.Write(dis[i][j] + " ");
Console.WriteLine();
}
}
}
public static void Main(String[] args)
{
int n = 6, m = 4;
for (int i = 0; i < N; i++)
gr[i] = new List<int>();
for (int i = 0; i < 2; i++)
dis[i] = new List<int>();
add_edge(1, 2);
add_edge(2, 3);
add_edge(2, 4);
add_edge(5, 6);
goodsets(n);
}
}
|
Javascript
<script>
var N = 100005;
var gr = Array.from(Array(N), ()=>Array());
var dis = Array.from(Array(2), ()=>Array());
var vis = Array(N).fill(false);
var color = Array(N).fill(0);
var bip;
function add_edge(x, y)
{
gr[x].push(y);
gr[y].push(x);
}
function dfs(x, col)
{
vis[x] = true;
color[x] = col;
for(var i of gr[x])
{
if (!vis[i])
dfs(i, col ^ 1);
else if (color[i] == col)
bip = false;
}
}
function goodsets(n)
{
bip = true;
for (var i = 1; i <= n; i++)
if (!vis[i])
dfs(i, 0);
if (!bip)
document.write(-1 + "<br>");
else
{
for (var i = 1;
i <= n; i++)
dis[color[i]].push(i);
for (var i = 0; i < 2; i++)
{
for (var j = 0;
j < dis[i].length; j++)
document.write(dis[i][j] + " ");
document.write("<br>")
}
}
}
var n = 6, m = 4;
add_edge(1, 2);
add_edge(2, 3);
add_edge(2, 4);
add_edge(5, 6);
goodsets(n);
</script>
|
Time Complexity: O(n)
Space Complexity: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...