Tan 30 Degrees

The value of tan 30 degrees is 1/2. In radians, tan 30° is written as tan π/6. In fraction form, the value of tan 30° is 1/√3, and in decimal form, the value is 0.577.

In this article, we are going to learn how to derive the value of tan 30 degrees and its use in trigonometric functions.

Tan 30 Degree Value

The value of tan 30 degrees is equal to 0.577. Converting degree to radian, that is, θ (radians) = θ × π/180° The value of tan 30 degrees is calculated by various methods, including the formula of the trigonometric ratio.

Tan A = Tan 30° = 1/√3

Tangent of 30 in Radians

The tangent of 30 degrees can be calculated in radians as well. Since 30 degrees is equivalent to π/6 radians (as 180∘ is π radians), the tangent of 30 degrees is the same as the tangent of π/6 radians.

The tangent of π/6 is:

tan(π/6)= √3/ 3​​

This value is derived from the properties of a 30-60-90 right triangle, where the tangent of 30 degrees (or π/6 radians) is the ratio of the opposite side to the adjacent side in such a triangle.

Tan 30 Degree Derivation

We can derive the value of tan 30 Degree using the graphical method.

Consider an equilateral triangle PQR where,

PQ = QR = RP and ∠P = ∠Q = ∠R = 60°. …………….(1)

Draw a perpendicular bisector PS of the line QR from vertex P.

Now, QS = RS, and PS = √3QS

In right angle triangle PQS

tan 30° = Perpendicular / Base

Here, 
Perpendicular = QS
Base = PS

tan 30° = QS / PS

tan 30° = 1/√3

Thus, the value of tan 30° is 1/√3

Value of Trigonometric Functions

Various values of trigonometric functions are used to solve complex functions. Basic values of trigonometric functions can be learned from the tale below:

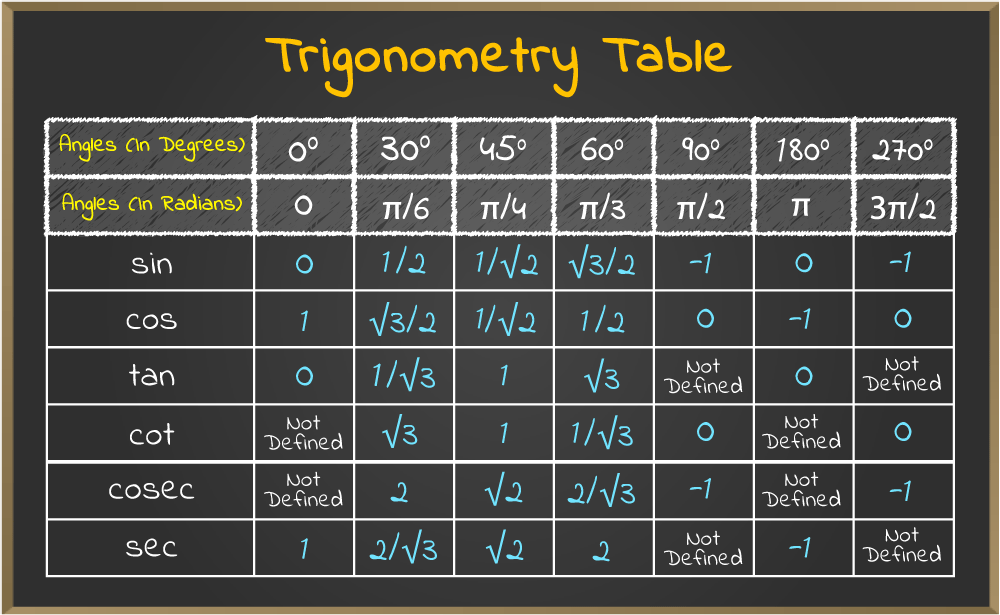
Tan 30 Degrees in Terms of Trigonometric Functions

Trigonometric functions are also called circular functions or trigonometric ratios. The relationship between angles and sides is represented by these trigonometric functions. The representation of the value of tan 30° using trigonometric functions are:

• Tan 30° = ± √(sec² 30° – 1)
• Tan 30° = 1/cot 30°

Solved Examples on Tan 30 Degree

Let’s solve some example problems on Tan 30 Degree.

Example 1: In a right-angle triangle, one angle is 30°, and the base for 30° is 3m. Find the length of the perpendicular.

Solution:

Given:  Base = 3m

Tan 30 = 1/√3

P/B = 1/√3   

P/3 = 1/√3   

p = √3  

Example 2: In a right triangle hypotenuse is 20 cm, and one side is 10√3 cm, find the angles of the triangle.

Solution:

Given: H = 20, and B = 10√3

Finding third side using pythagoras theorem.

P² + B² = H² 

P² + (10√3)² = 20²

p² + 300 = 400

P² = 100

p = 10

The third side is 10cm. The ratio of the two sides 10cm and 10√3cm is 1/√3,  So there must be an angle of 30° in triangle Since the triangle is a right angle, so the third angle is

90° – 30° = 60°

The Angles of a triangle are 30°, 60°, 90°.

Tan 30 Degree- FAQs

Write the value of tan 30°.

The value of tan 30 degrees is 1/√3

Write the value of 30 degrees in radians.

The value of 30 degrees in radian is π/6.

Write the value of sin 30 degree and cos 30 degree.

The value of sin 30° is 1/2 and the value of cos 30° is √3/2

Write the formula of tan function.

In a right-angle triangle tan of an angle, is equal to the ratio of the opposite side of the angle and the base of a right-angle triangle.

i.e tan A = Opposite Side(Perpendicular)/Base Side.

How to find the value of tan 30 degrees from a practical approach?

The value of tan 30 can be found using a practical approach by drawing a right-angled triangle having an angle of 30 with the help of a compass, protector, and ruler. After the triangle is drawn, take the ratio of the adjacent side to the base. The value obtained is the value of tan 30.

Tan 30° = 0.577