Find the total Number of Digits in (N!)N
Last Updated :
26 Jul, 2022
Given a number N. The task is to find the total number of Digits in 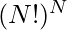 .
.
Examples:
Input: N = 3
Output: 3
If N=3, (3!)3=216,
So the count of digits is 3
Input: N = 4
Output: 6
Approach:
As we know,
log(a*b) = log(a) + log(b)
Consider,
X = log(N!) = log(1*2*3....... * N)
= log(1)+log(2)+........ +log(N)
Now, we know that the floor value of log base 10 increased by 1, of any number, which gives the number of digits present in that number. That is, the number of digits in a number say N will be floor(log10N) + 1. Therefore, the number of digits in 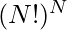 will be:
will be:
floor(log(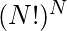 ))+1= floor(N*log10(N!)) + 1= floor(N*X) + 1.
))+1= floor(N*log10(N!)) + 1= floor(N*X) + 1.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int CountDigits(int n)
{
if (n == 1)
return 1;
double sum = 0;
for (int i = 2; i <= n; ++i) {
sum += (double)log(i) / (double)log(10);
}
sum *= (double)n;
return ceil(sum);
}
int main()
{
int N = 5;
cout << CountDigits(N);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
import java.lang.*;
class GFG
{
public double CountDigits(int n)
{
if (n == 1)
return 1;
double sum = 0;
for (int i = 2; i <= n; ++i)
{
sum += ((double)Math.log(i) /
(double)Math.log(10));
}
sum *= n;
return Math.ceil(sum);
}
public static void main(String args[])
{
GFG g = new GFG();
int N = 5;
System.out.println(g.CountDigits(N));
}
}
|
Python3
import math as ma
def CountDigits(n):
if(n==1):
return 1
sum=0
for i in range(2,n+1):
sum+=ma.log(i,10)
sum*=n
return ma.ceil(sum)
if __name__=='__main__':
N=5
print(CountDigits(N))
|
C#
using System;
class GFG
{
public double CountDigits(int n)
{
if (n == 1)
return 1;
double sum = 0;
for (int i = 2; i <= n; ++i)
{
sum += ((double)Math.Log(i) /
(double)Math.Log(10));
}
sum *= n;
return Math.Ceiling(sum);
}
public static void Main()
{
GFG g = new GFG();
int N = 5;
Console.WriteLine(g.CountDigits(N));
}
}
|
PHP
<?php
function CountDigits($n)
{
if ($n == 1)
return 1;
$sum = 0;
for ($i = 2; $i <= $n; ++$i)
{
$sum += log($i) / log(10);
}
$sum *= $n;
return ceil($sum);
}
$N = 5;
echo CountDigits($N);
?>
|
Javascript
<script>
function CountDigits(n) {
if (n == 1)
return 1;
var sum = 0;
for (i = 2; i <= n; ++i) {
sum += (Math.log(i) / Math.log(10));
}
sum *= n;
return Math.ceil(sum);
}
var N = 5;
document.write(CountDigits(N));
</script>
|
Time Complexity: O(n) // n is the length of the array.
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...