Find the super power of a given Number
Last Updated :
02 Dec, 2021
Given an integer 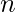 . The task is to find the superpower from the factorization of
. The task is to find the superpower from the factorization of 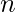 .
.
The Superpower is the highest power among the power of primes in the factorisation of a number n.
Examples:
Input : n = 32
Output : 5
Input : n = 240
Output : 4
For finding the superpower of any given number 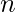 , we have to complete the factorisation of n, and find out highest power among all of the prime factors.
, we have to complete the factorisation of n, and find out highest power among all of the prime factors.
Note: Using Sieve for the purpose of storing list of primes is useful in terms of optimization.
Algorithm :
- Iterate over primes and calculate the factorization of n.
- For each prime among the stored list of primes and which is also a factor of n,
find its power and check it for super power.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#define MAX 100000
using namespace std;
bool prime[100002];
void SieveOfEratosthenes()
{
memset(prime, true, sizeof(prime));
for (int p = 2; p * p <= MAX; p++)
if (prime[p] == true)
for (int i = p * 2; i <= MAX; i += p)
prime[i] = false;
}
int superpower(int n)
{
SieveOfEratosthenes();
int superPower = 0, factor = 0;
int i = 2;
while (n > 1 && i <= MAX) {
if (prime[i]) {
factor = 0;
while (n % i == 0 && n > 1) {
factor++;
n = n / i;
}
if (superPower < factor)
superPower = factor;
}
i++;
}
return superPower;
}
int main()
{
int n = 256;
cout << superpower(n);
return 0;
}
|
Java
class GFG{
static int MAX=100000;
static boolean[] prime=new boolean[100002];
static void SieveOfEratosthenes()
{
for (int p = 2; p * p <= MAX; p++)
if (prime[p] == false)
for (int i = p * 2; i <= MAX; i += p)
prime[i] = true;
}
static int superpower(int n)
{
SieveOfEratosthenes();
int superPower = 0, factor = 0;
int i = 2;
while (n > 1 && i <= MAX) {
if (!prime[i]) {
factor = 0;
while (n % i == 0 && n > 1) {
factor++;
n = n / i;
}
if (superPower < factor)
superPower = factor;
}
i++;
}
return superPower;
}
public static void main(String[] args)
{
int n = 256;
System.out.println(superpower(n));
}
}
|
Python3
MAX = 100000;
prime = [True] * 100002;
def SieveOfEratosthenes():
p = 2;
while(p * p <= MAX):
if (prime[p] == True):
i = p * 2;
while(i <= MAX):
prime[i] = False;
i += p;
p += 1;
def superpower(n):
SieveOfEratosthenes();
superPower = 0;
factor = 0;
i = 2;
while (n > 1 and i <= MAX):
if (prime[i]):
factor = 0;
while (n % i == 0 and n > 1):
factor += 1;
n = int(n / i);
if (superPower < factor):
superPower = factor;
i += 1;
return superPower;
n = 256;
print(superpower(n));
|
C#
class GFG
{
static int MAX = 100000;
static bool[] prime = new bool[100002];
static void SieveOfEratosthenes()
{
for (int p = 2;
p * p <= MAX; p++)
if (prime[p] == false)
for (int i = p * 2;
i <= MAX; i += p)
prime[i] = true;
}
static int superpower(int n)
{
SieveOfEratosthenes();
int superPower = 0, factor = 0;
int i = 2;
while (n > 1 && i <= MAX)
{
if (!prime[i])
{
factor = 0;
while (n % i == 0 && n > 1)
{
factor++;
n = n / i;
}
if (superPower < factor)
superPower = factor;
}
i++;
}
return superPower;
}
static void Main()
{
int n = 256;
System.Console.WriteLine(superpower(n));
}
}
|
PHP
<?php
$MAX = 100000;
$prime = array_fill(0, 100002, true);
function SieveOfEratosthenes()
{
global $MAX, $prime;
for ($p = 2; $p * $p <= $MAX; $p++)
if ($prime[$p] == true)
for ($i = $p * 2;
$i <= $MAX; $i += $p)
$prime[$i] = false;
}
function superpower($n)
{
SieveOfEratosthenes();
global $MAX, $prime;
$superPower = 0;
$factor = 0;
$i = 2;
while ($n > 1 && $i <= $MAX)
{
if ($prime[$i])
{
$factor = 0;
while ($n % $i == 0 && $n > 1)
{
$factor++;
$n = $n / $i;
}
if ($superPower < $factor)
$superPower = $factor;
}
$i++;
}
return $superPower;
}
$n = 256;
echo superpower($n);
?>
|
Javascript
<script>
var MAX = 100000;
var prime = Array(100002).fill(true);
function SieveOfEratosthenes()
{
for (var p = 2; p * p <= MAX; p++)
if (prime[p] == true)
for (var i = p * 2; i <= MAX; i += p)
prime[i] = false;
}
function superpower(n)
{
SieveOfEratosthenes();
var superPower = 0, factor = 0;
var i = 2;
while (n > 1 && i <= MAX) {
if (prime[i]) {
factor = 0;
while (n % i == 0 && n > 1) {
factor++;
n = n / i;
}
if (superPower < factor)
superPower = factor;
}
i++;
}
return superPower;
}
var n = 256;
document.write( superpower(n));
</script>
|
Share your thoughts in the comments
Please Login to comment...