Find the Sum of the series 1 + 1/3 + 1/5 + 1/7 + … till N terms
Last Updated :
19 Aug, 2022
Given a number N, the task is to find the sum of the below series till N terms.
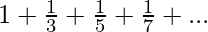
Examples:
Input: N = 10
Output: 2.133256
Explanation:
The sum of series 1 + 1/3 + 1/5 + 1/7 + 1/9 + 1/11 is 2.133256.
Input: N = 20
Output: 2.479674
Explanation:
The sum of series 1 + 1/3 + 1/5 + 1/7 + … + 1/41 is 2.479674.
Approach: From the given series, find the formula for Nth term:
1st term = 1
2nd term = 1/3
3rd term = 1/5
4th term = 1/7
.
.
Nthe term = 1 / (2 * N - 1))
Therefore:
Nth term of the series
*** QuickLaTeX cannot compile formula:
*** Error message:
Error: Nothing to show, formula is empty
Then iterate over numbers in the range [1, N] to find all the terms using the above formula and compute their sum.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void printSumSeries(int N)
{
float sum = 0;
for (int i = 1; i <= N; i++) {
sum += 1.0 / (2 * i - 1);
}
cout << sum << endl;
}
int main()
{
int N = 6;
printSumSeries(N);
return 0;
}
|
Java
class GFG {
static void printSumSeries(int N)
{
float sum = 0;
for (int i = 1; i <= N; i++) {
sum += 1.0 / (2 * i - 1);
}
System.out.println(sum);
}
public static void main (String[] args)
{
int N = 6;
printSumSeries(N);
}
}
|
Python3
def printSumSeries(N) :
sum = 0;
for i in range(1, N + 1) :
sum += 1.0 / (2 * i - 1);
print(sum);
if __name__ == "__main__" :
N = 6;
printSumSeries(N);
|
C#
using System;
class GFG {
static void printSumSeries(int N)
{
float sum = 0;
for (int i = 1; i <= N; i++) {
sum += (float)1.0 / (2 * i - 1);
}
Console.WriteLine(sum);
}
public static void Main (string[] args)
{
int N = 6;
printSumSeries(N);
}
}
|
Javascript
<script>
function printSumSeries( N)
{
let sum = 0;
for (let i = 1; i <= N; i++) {
sum += 1.0 / (2 * i - 1);
}
document.write(sum.toFixed(5));
}
let N = 6;
printSumSeries(N);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...