Find the sum of series 3, 7, 13, 21, 31….
Last Updated :
31 Aug, 2022
Given a number N. The task is to find the sum of below series upto nth term.
3, 7, 13, 21, 31, ….
Examples:
Input : N = 3
Output : 23
Input : N = 25
Output : 5875
Approach:
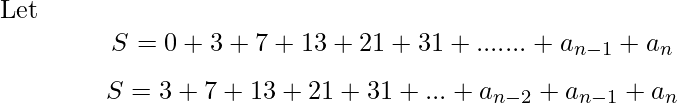
Subtracting the above two equations, we have:
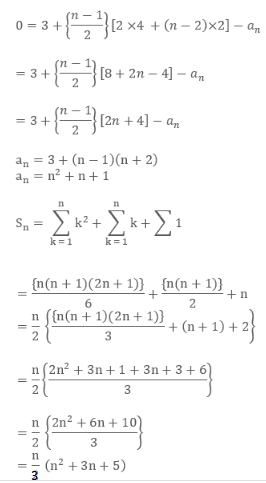
Below is the implementation of the above approach:
C++
#include <iostream>
#include <math.h>
using namespace std;
int findSum(int n)
{
return (n * (pow(n, 2) + 3 * n + 5)) / 3;
}
int main()
{
int n = 25;
cout << findSum(n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int calculateSum(int n)
{
return (n * ((int)Math.pow(n, 2) + 3 *
n + 5)) / 3;
}
public static void main(String arr[])
{
int n = 25;
System.out.println(calculateSum(n));
}
}
|
Python 3
def findSum(n):
return (n*(pow(n, 2)+3 * n + 5))/3
n = 25
print(int(findSum(n)))
|
C#
using System;
class GFG
{
static int calculateSum(int n)
{
return (n * ((int)Math.Pow(n, 2) + 3 *
n + 5)) / 3;
}
public static void Main()
{
int n = 25;
Console.WriteLine(calculateSum(n));
}
}
|
PHP
<?php
function findSum($n)
{
return ($n * (pow($n, 2) +
3 * $n + 5)) / 3;
}
$n = 25;
echo findSum($n);
?>
|
Javascript
<script>
function calculateSum(n)
{
return (n * (parseInt(Math.pow(n, 2) + 3 *
n + 5)) / 3);
}
var n = 25;
document.write(calculateSum(n));
</script>
|
Time Complexity : O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...