Find the sum of remaining sticks after each iterations
Last Updated :
03 Feb, 2023
Given N number of sticks of varying lengths in an array arr, the task is to determine the sum of the count of sticks that are left after each iteration. At each iteration, cut the length of the shortest stick from remaining sticks.
Examples:
Input: N = 6, arr = {5, 4, 4, 2, 2, 8}
Output: 7
Explanation:
Iteration 1:
Initial arr = {5, 4, 4, 2, 2, 8}
Shortest stick = 2
arr with reduced length = {3, 2, 2, 0, 0, 6}
Remaining sticks = 4
Iteration 2:
arr = {3, 2, 2, 4}
Shortest stick = 2
Left stick = 2
Iteration 3:
arr = {1, 2}
Shortest stick = 1
Left stick = 1
Iteration 4:
arr = {1}
Min length = 1
Left stick = 0
Input: N = 8, arr = {1, 2, 3, 4, 3, 3, 2, 1}
Output: 11
Approach: The approach to solving this problem is to sort the array and then find the number of minimum length sticks that are of the same length while traversing and update the sum accordingly at each step and in the end return the sum.
C++
#include <bits/stdc++.h>
using namespace std;
int sum(vector<int> &arr, int n)
{
int sum = 0;
sort(arr.begin(),arr.end());
int prev=0,count=1,s=arr.size();
int i=1;
while(i<arr.size()){
if(arr[i]==arr[prev]){
count++;
}else{
prev=i;
sum+=s-count;
s-=count;
count=1;
}
i++;
}
return sum;
}
int main()
{
int n = 6;
vector<int> ar{ 5, 4, 4, 2, 2, 8 };
int ans = sum(ar, n);
cout << ans << '\n';
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
public static int sum(int arr[], int n)
{
int sum = 0;
Arrays.sort(arr);
int prev = 0, count = 1, s = n;
int i = 1;
while (i < n)
{
if (arr[i] == arr[prev])
{
count++;
}
else
{
prev = i;
sum += s - count;
s -= count;
count = 1;
}
i++;
}
return sum;
}
public static void main(String[] args)
{
int n = 6;
int ar[] = { 5, 4, 4, 2, 2, 8 };
int ans = sum(ar, n);
System.out.println(ans);
}
}
|
Python3
def sum(arr, n):
sum = 0
arr.sort()
prev, count, s = 0, 1, n
i = 1
while (i < n):
if (arr[i] == arr[prev]):
count += 1
else:
prev = i
sum += s - count
s -= count
count = 1
i += 1
return sum
n = 6
ar = [ 5, 4, 4, 2, 2, 8 ]
ans = sum(ar, n)
print(ans)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public static int sum(int[] arr, int n)
{
int sum = 0;
Array.Sort(arr);
int prev = 0, count = 1, s = n;
int i = 1;
while (i < n)
{
if (arr[i] == arr[prev])
{
count++;
}
else
{
prev = i;
sum += s - count;
s -= count;
count = 1;
}
i++;
}
return sum;
}
public static void Main (String[] args)
{
int n = 6;
int[] ar = { 5, 4, 4, 2, 2, 8 };
int ans = sum(ar, n);
Console.WriteLine(ans);
}
}
|
Javascript
<script>
function sum(arr,n)
{
let sum = 0;
arr.sort();
let prev = 0, count = 1, s = n;
let i = 1;
while (i < n)
{
if (arr[i] == arr[prev])
{
count++;
}
else
{
prev = i;
sum += s - count;
s -= count;
count = 1;
}
i++;
}
return sum;
}
let n = 6;
let ar = [ 5, 4, 4, 2, 2, 8 ];
let ans = sum(ar, n);
document.write(ans);
</script>
|
Time Complexity: O(Nlog(N)) where N is the number of sticks.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Another Approach:
- Store the frequency of stick lengths in a map
- In each iteration,
- Find the frequency of min length’s stick
- Decrease the frequency of min length’s stick from each stick’s frequency
- Add the count of non-zero sticks to the resultant stick.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int sum(int ar[], int n)
{
map<int, int> mp;
for (int i = 0; i < n; i++) {
mp[ar[i]]++;
}
int sum = 0;
for (auto p : mp) {
n -= p.second;
sum += n;
}
return sum;
}
int main()
{
int n = 6;
int ar[] = { 5, 4, 4, 2, 2, 8 };
int ans = sum(ar, n);
cout << ans << '\n';
return 0;
}
|
Java
import java.util.HashMap;
import java.util.Map;
class GFG
{
static int sum(int ar[], int n)
{
HashMap<Integer,
Integer> mp = new HashMap<>();
for (int i = 0; i < n; i++)
{
mp.put(ar[i], 0);
}
for (int i = 0; i < n; i++)
{
mp.put(ar[i], mp.get(ar[i]) + 1) ;
}
int sum = 0;
for(Map.Entry p : mp.entrySet())
{
n -= (int)p.getValue();
sum += n;
}
return sum;
}
public static void main (String[] args)
{
int n = 6;
int ar[] = { 5, 4, 4, 2, 2, 8 };
int ans = sum(ar, n);
System.out.println(ans);
}
}
|
Python3
def sum(ar, n):
mp = dict()
for i in ar:
if i in mp:
mp[i]+= 1
else:
mp[i] = 1
mp = sorted(list(mp.items()))
sum = 0
for pair in mp:
n-= pair[1]
sum+= n
return sum
def main():
n = 6
ar = [5, 4, 4, 2, 2, 8]
ans = sum(ar, n)
print(ans)
main()
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int sum(int []ar, int n)
{
SortedDictionary<int,
int> mp = new SortedDictionary<int,
int>();
for (int i = 0; i < n; i++)
{
if(!mp.ContainsKey(ar[i]))
mp.Add(ar[i], 0);
else
mp[ar[i]] = 0;
}
for (int i = 0; i < n; i++)
{
if(!mp.ContainsKey(ar[i]))
mp.Add(ar[i], 1);
else
mp[ar[i]] = ++mp[ar[i]];
}
int sum = 0;
foreach(KeyValuePair<int, int> p in mp)
{
n -= p.Value;
sum += n;
}
return sum;
}
public static void Main (String[] args)
{
int n = 6;
int []ar = { 5, 4, 4, 2, 2, 8 };
int ans = sum(ar, n);
Console.WriteLine(ans);
}
}
|
Javascript
<script>
function sum(ar, n)
{
let mp = new Map();
for (let i = 0; i < n; i++)
{
mp.set(ar[i], 0);
}
for (let i = 0; i < n; i++)
{
mp.set(ar[i], mp.get(ar[i]) + 1);
}
mp = new Map([...mp].sort((a, b) => String(a[0]).localeCompare(b[0])))
let sum = 0;
for (let p of mp)
{
n -= p[1]
sum += n;
}
return sum;
}
let n = 6;
let ar = [5, 4, 4, 2, 2, 8];
let ans = sum(ar, n);
document.write(ans + '<br>');
</script>
|
Time Complexity: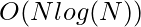 where N is the number of sticks
where N is the number of sticks
Auxiliary Space: O(N), where N is the number of sticks.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...