Find the sum of N terms of the series 1, 4, 13, 40, 121, …
Last Updated :
16 Aug, 2022
Given a positive integer, n. Find the sum of the first n term of the series:
1, 4, 13, 40, 121, …..
Examples:
Input: n = 5
Output: 179
Input: n = 3
Output: 18
Approach:
The sequence is formed by using the following pattern. For any value N-
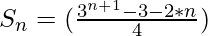
The above solution can be derived following the series of steps-
Let Tn be the nth term and Sn be the sum to n terms of the given series.
Thus, we have
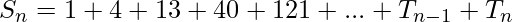 -(1)
-(1)
Equation (1) can be written as-
S_{n}=1+4+13+40+121+…+T_{n-1}+T_{n} -(2)
Subtracting equation (2) from equation (1), we get
![Rendered by QuickLaTeX.com 0=1+[3+9+27+81+...+(T_{n}-T_{n-1})-T_{n}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-71557ee1efdfa7980e4c02712052ae90_l3.png)
The above equation 3, 9, 27, 81, … is a G.P. with common ratio 3 and first term 3.
Thus, we have
![Rendered by QuickLaTeX.com 1+[\frac{3*(3^{n-1}-1)}{3-1}]-T_{n}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a8bf40874578f3b97fddc38551697ba_l3.png)
![Rendered by QuickLaTeX.com 1+[\frac{3*(3^{n-1}-1)}{2}]-T_{n}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d28e5db53c98b2d62eec29ee3214c66_l3.png)
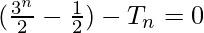
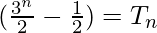
Since,
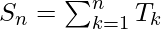
Therefore,
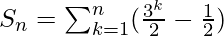
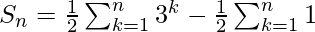
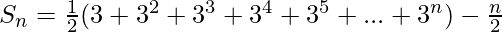
![Rendered by QuickLaTeX.com S_{n}=\frac{1}{2}[\frac{3*(3^{n}-1)}{2}]-\frac{n}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3ef1fb710ff8da3cfc48f62ef9bff299_l3.png)
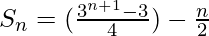
Thus, sum of n terms is
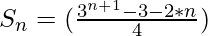
Illustration:
Input: n = 5
Output: 179
Explanation:
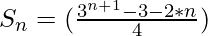
=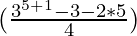
=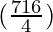
=179
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findSum(int N)
{
return (pow(3, N + 1) -
3 - 2 * N) / 4;
}
int main()
{
int N = 5;
cout << findSum(N);
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static int findSum(int N)
{
return (int)(Math.pow(3, N + 1) -
3 - 2 * N) / 4;
}
public static void main(String args[])
{
int N = 5;
System.out.print(findSum(N));
}
}
|
Python3
def findSum(N):
return (3 ** (N + 1) - 3 - 2 * N) // 4;
N = 5;
print(findSum(N));
|
C#
using System;
class GFG
{
static int findSum(int N)
{
return (int)(Math.Pow(3, N + 1) -
3 - 2 * N) / 4;
}
public static void Main()
{
int N = 5;
Console.Write(findSum(N));
}
}
|
Javascript
<script>
function findSum(N) {
return Math.floor((Math.pow(3, N + 1) -
3 - 2 * N) / 4);
}
let N = 5;
document.write(findSum(N));
</script>
|
Time Complexity: O(log3N) because using inbuilt pow function
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...