Find the sum of infinite series 1^2.x^0 + 2^2.x^1 + 3^2.x^2 + 4^2.x^3 +…….
Last Updated :
31 Aug, 2022
Given an infinite series and a value x, the task is to find its sum. Below is the infinite series
1^2*x^0 + 2^2*x^1 + 3^2*x^2 + 4^2*x^3 +……. upto infinity, where x belongs to (-1, 1)
Examples:
Input: x = 0.5
Output: 12
Input: x = 0.9
Output: 1900
Approach:
Though the given series is not an Arithmetico-Geometric series, however, the differences 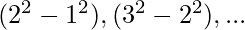 and so on, forms an AP. So, we can use the Method of Differences.
and so on, forms an AP. So, we can use the Method of Differences.

Hence, the sum will be (1+x)/(1-x)^3.
Below is the implementation of above approach:
C++
#include <iostream>
#include <math.h>
using namespace std;
double solve_sum(double x)
{
return (1 + x) / pow(1 - x, 3);
}
int main()
{
double x = 0.5;
cout << solve_sum(x);
return 0;
}
|
Java
import java.util.*;
class solution
{
static double calculateSum(double x)
{
return (1 + x) / Math.pow(1 - x, 3);
}
public static void main(String ar[])
{
double x=0.5;
System.out.println((int)calculateSum(x));
}
}
|
Python
def solve_sum(x):
return (1 + x)/pow(1-x, 3)
x = 0.5
print(int(solve_sum(x)))
|
C#
using System;
class GFG
{
static double calculateSum(double x)
{
return (1 + x) / Math.Pow(1 - x, 3);
}
public static void Main()
{
double x = 0.5;
Console.WriteLine((int)calculateSum(x));
}
}
|
PHP
<?php
function solve_sum($x)
{
return (1 + $x) /
pow(1 - $x, 3);
}
$x = 0.5;
echo solve_sum($x);
?>
|
Javascript
<script>
function calculateSum(x)
{
return (1 + x) / Math.pow(1 - x, 3);
}
var x=0.5;
document.write(parseInt(calculateSum(x)));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...