Find the sum of first N terms of the series 2, 5, 8, 11, 14..
Last Updated :
19 Apr, 2023
Given a positive integer N, the task is to find the sum of the first N terms of the series
2, 5, 8, 11, 14..
Examples:
Input: N = 5
Output: 40
Input: N = 10
Output: 155
Approach:
1st term = 2
2nd term = (2 + 3) = 5
3rd term = (5 + 3) = 8
4th term = (8 + 3) = 11
.
.
Nth term = (2 + (N – 1) * 3) = 3N – 1
The sequence is formed by using the following pattern. For any value N-
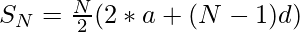
Here,
a is the first term
d is the common difference
The above solution can be derived following the series of steps-
The series-
2, 5, 8, 11, …., till N terms
is in A.P. with first term of the series a = 2 and common difference d = 3
Sum of N terms of an A.P. is
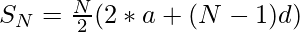
Illustration:
Input: N = 5
Output: 40
Explanation:
a = 2
d = 3
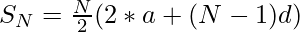
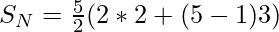
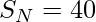
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
int nth(int n, int a1, int d)
{
return (a1 + (n - 1) * d);
}
int sum(int a1, int nterm, int n)
{
return n * (a1 + nterm) / 2;
}
int main()
{
int N = 5;
int a = 2;
int d = 3;
int nterm = nth(N, a, d);
cout << sum(a, nterm, N) << endl;
return 0;
}
|
C
#include <stdio.h>
int nth(int n, int a1, int d)
{
return (a1 + (n - 1) * d);
}
int sum(int a1, int nterm, int n)
{
return n * (a1 + nterm) / 2;
}
int main()
{
int N = 5;
int a = 2;
int d = 3;
int nterm = nth(N, a, d);
printf("%d", sum(a, nterm, N));
return 0;
}
|
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int N = 5;
int a = 2;
int d = 3;
int nterm = nth(N, a, d);
System.out.println(sum(a, nterm, N));
}
public static int nth(int n,
int a1, int d)
{
return (a1 + (n - 1) * d);
}
public static int sum(int a1,
int nterm, int n)
{
return n * (a1 + nterm) / 2;
}
}
|
Python3
def nth(n, a1, d):
return (a1 + (n - 1) * d);
def sum(a1, nterm, n):
return n * (a1 + nterm) / 2;
N = 5;
a = 2;
d = 3;
nterm = nth(N, a, d);
print((int)(sum(a, nterm, N)))
|
C#
using System;
public class GFG
{
public static int nth(int n, int a1, int d)
{
return (a1 + (n - 1) * d);
}
public static int sum(int a1, int nterm, int n)
{
return n * (a1 + nterm) / 2;
}
static public void Main()
{
int N = 5;
int a = 2;
int d = 3;
int nterm = nth(N, a, d);
Console.Write(sum(a, nterm, N));
}
}
|
Javascript
<script>
function nth(n, a1, d) {
return (a1 + (n - 1) * d);
}
function sum(a1, nterm, n) {
return n * (a1 + nterm) / 2;
}
let N = 5;
let a = 2;
let d = 3;
let nterm = nth(N, a, d);
document.write(sum(a, nterm, N) + '<br>');
</script>
|
Time complexity: O(1) because performing constant operations
Auxiliary Space: O(1) // since no extra array or recursion is used so the space taken by the algorithm is constant
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...