Find the sum of all multiples of 2 and 5 below N

Given a number N. and the task is to find the sum of all multiples of 2 and 5 below N ( N may be up to 10^10). 

Examples:  

Input : N = 10
Output : 25
Explanation : 2 + 4 + 6 + 8 + 5

Input : N = 20
Output : 110

Approach :

We know that multiples of 2 form an AP as: 

2, 4, 6, 8, 10, 12, 14….(1) 

Similarly, multiples of 5 form an AP as: 

5, 10, 15……(2) 

Now, Sum(1) + Sum(2) = 2, 4, 5, 6, 8, 10, 10, 12, 14, 15….
Here, 10 is repeated. In fact, all of the multiples of 10 or 2*5 are repeated because it is counted twice, once in the series of 2 and again in the series of 5. Hence we’ll subtract the sum of the series of 10 from Sum(1) + Sum(2).

The formula for the sum of an A.P is :  

n * ( a + l ) / 2
Where 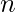is the number of terms, 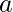is the starting term, and 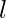is the last term. 

So, the final answer is:  

S₂ + S₅ – S₁₀

Below is the implementation of the above approach:  

C++

// CPP program to find the sum of all
// multiples of 2 and 5 below N

#include <bits/stdc++.h>
using namespace std;

// Function to find sum of AP series
long long sumAP(long long n, long long d)
{
    // Number of terms
    n /= d;

    return (n) * (1 + n) * d / 2;
}

// Function to find the sum of all
// multiples of 2 and 5 below N
long long sumMultiples(long long n)
{
    // Since, we need the sum of
    // multiples less than N
    n--;

    return sumAP(n, 2) + sumAP(n, 5) - sumAP(n, 10);
}

// Driver code
int main()
{
    long long n = 20;

    cout << sumMultiples(n);

    return 0;
}

C

// C program to find the sum of all
// multiples of 2 and 5 below N
#include <stdio.h>

// Function to find sum of AP series
long long sumAP(long long n, long long d)
{
    // Number of terms
    n /= d;

    return (n) * (1 + n) * d / 2;
}

// Function to find the sum of all
// multiples of 2 and 5 below N
long long sumMultiples(long long n)
{
    // Since, we need the sum of
    // multiples less than N
    n--;

    return sumAP(n, 2) + sumAP(n, 5) - sumAP(n, 10);
}

// Driver code
int main()
{
    long long n = 20;

    printf("%lld",sumMultiples(n));

    return 0;
}

// This code is contributed by kothavvsaakash.

Java

// Java program to find the sum of all
// multiples of 2 and 5 below N

class GFG{
// Function to find sum of AP series
static long sumAP(long n, long d)
{
    // Number of terms
    n /= d;

    return (n) * (1 + n) * d / 2;
}

// Function to find the sum of all
// multiples of 2 and 5 below N
static long sumMultiples(long n)
{
    // Since, we need the sum of
    // multiples less than N
    n--;

    return sumAP(n, 2) + sumAP(n, 5) - sumAP(n, 10);
}

// Driver code
public static void main(String[] args)
{
    long n = 20;

    System.out.println(sumMultiples(n));
}
}
// This code is contributed by mits

Python3

# Python3 program to find the sum of
# all multiples of 2 and 5 below N

# Function to find sum of AP series
def sumAP(n, d):

    # Number of terms
    n = int(n / d);

    return (n) * (1 + n) * (d / 2);

# Function to find the sum of all
# multiples of 2 and 5 below N
def sumMultiples(n):

    # Since, we need the sum of
    # multiples less than N
    n -= 1;

    return (int(sumAP(n, 2) + sumAP(n, 5) -
                              sumAP(n, 10)));

# Driver code
n = 20;

print(sumMultiples(n));

# This code is contributed by mits

C#

// C# program to find the sum of all
// multiples of 2 and 5 below N

using System;

public class GFG{

    // Function to find sum of AP series
static long sumAP(long n, long d)
{
    // Number of terms
    n /= d;

    return (n) * (1 + n) * d / 2;
}

// Function to find the sum of all
// multiples of 2 and 5 below N
static long sumMultiples(long n)
{
    // Since, we need the sum of
    // multiples less than N
    n--;

    return sumAP(n, 2) + sumAP(n, 5) - sumAP(n, 10);
}

// Driver code

    static public void Main (){
            long n = 20;

        Console.WriteLine(sumMultiples(n));
    }
}

PHP

<?php
// PHP program to find the sum of all
// multiples of 2 and 5 below N
// Function to find sum of AP series
function sumAP($n, $d)
{
    // Number of terms
    $n = (int)($n /$d);

    return ($n) * ((1 + $n) *
                   (int)$d / 2);
}

// Function to find the sum of all
// multiples of 2 and 5 below N
function sumMultiples($n)
{
    // Since, we need the sum of
    // multiples less than N
    $n--;

    return sumAP($n, 2) + sumAP($n, 5) -
                          sumAP($n, 10);
}

// Driver code
$n = 20;

echo sumMultiples($n);

// This code is contributed
// by Sach_Code
?>

Javascript

<script>

// Java script program to find the sum of all
// multiples of 2 and 5 below N

// Function to find sum of AP series
function sumAP(n, d)
{

    // Number of terms
    n = parseInt(n / d);

    return (n) * ((1 + n) *
         parseInt(d) / 2);
}

// Function to find the sum of all
// multiples of 2 and 5 below N
function sumMultiples(n)
{

    // Since, we need the sum of
    // multiples less than N
    n--;

    return sumAP(n, 2) + sumAP(n, 5) -
           sumAP(n, 10);
}

// Driver code
n = 20;

document.write( sumMultiples(n));

// This code is contributed by bobby

</script>

Output:

110

Time complexity: O(1), since there is no loop or recursion.

Auxiliary Space: O(1), since no extra space has been taken.