The arithmetic value which is used for representing the quantity and used in making calculations are defined as Numbers. A symbol like “4,5,6” which represents a number is known as numerals. Without numbers, we can’t do counting of things, date, time, money, etc. these numbers are also used for measurement and used for labeling.
The properties of numbers make them helpful in performing arithmetic operations on them. These numbers can be written in numeric forms and also in words.
For example, 3 is written as three in words, 35 is written as thirty-five in words, etc. Students can write the numbers from 1 to 100 in words to learn more.
There are different types of numbers, which we can learn. They are whole and natural numbers, odd and even numbers, rational and irrational numbers, etc
What is Number System?
A Number System is a method of showing numbers by writing, which is a mathematical way of representing the numbers of a given set, by using the numbers or symbols in a mathematical manner. The writing system for denoting numbers using digits or symbols in a logical manner is defined as Number System.
We can use the digits from 0 to 9 to form all the numbers. With these digits, anyone can create infinite numbers.
For example, 156,3907, 3456, 1298, 784859 etc
What is a Square Root?
The value of the number of square roots, which on multiplication by itself gives the original number. Suppose, a is the square root of b, then it is represented as a=√b or we can express the same equation as a2 = b. Here,’√’ this symbol we used to represent the root of numbers is termed as radical. The positive number when it is to be multiplied by itself represents the square of the number. The square root of the square of any positive number gives the original number.
For example, the square of 4 is 16, 42 = 16, and the square root of 16, √16 = 4. Since 4 is a perfect square, hence it is easy to find the square root of such numbers, but for an imperfect square, it’s really tricky.
Square Root is represented as ‘√’. It is called a radical symbol. To represent a number ‘a’ as a square root using this symbol can be written as ‘√a‘, where a is the number.
The number here under the radical symbol is called the radicand. For example, the square root of 4 is also represented as a radical of 4. Both represent the same value.
and The formula to find the square root is: b = √a
Properties of Square Root
It is defined as a one-to-one function that takes a positive number as an input and returns the square root of the given input number.
f(x) = √x
For example, here if x = 9, then the function returns the output value as 3.
These are properties of the square root are as follows:
- If a number is a perfect square number, then there definitely exists a perfect square root.
- If a number ends with an even number of zeros (0’s), then we can have a square root.
- The two square root values can be multiplied. For example, √3 can be multiplied by √2, then the result will be √6.
- When two same square roots are multiplied, then the result must be a radical number. It shows that the result is a non-square root number. For example, when √7 is multiplied by √7, the result obtained is 7.
- The square root of negative numbers is undefined. hence the perfect square cannot be negative.
- Some of a number ends with 2, 3, 7 or 8 (in the unit digit), then the perfect square root does not exist.
- Some of a number ends with 1, 4, 5, 6 or 9 in the unit digit, then the number will have a square root.
Methods to Find Square Root
It is easy to find the square root of a number that is a perfect square.
Perfect squares are those positive numbers that can be written as the multiplication of a number by itself. or you can say that perfect squares are numbers which is the value of power 2 of any integer.
We can use four methods to find the square root of numbers and these methods are as:
- Repeated Subtraction Method of Square Root
- Square Root by Prime Factorization Method
- Square Root by Estimation Method
- Square Root by Long Division Method
The above three methods can be conveniently used for perfect squares, while the fourth method, i.e long division method can be used for all numbers whether it is a perfect square or not.
Repeated Subtraction Method of Square Root
It’s a very simple method, here we will subtract the consecutive odd numbers from the number for which we are finding the square root till we reach 0. In this method, the number of times we subtract is the square root of the given number. This method works for perfect square numbers only. Let us find the square root of 25 using this method.
Example:
25 – 1 = 24
24 – 3 = 21
21 – 5 = 16
16 – 7 = 9
9 – 9 = 0
Here we have subtracted 5 times so the perfect square root of 25 is 5
Square Root by Prime Factorization Method
Prime factorization of any number means to represent that particular number as a product of prime numbers. To find the square root of a given number through the prime factorization method, Some steps need to be followed:
Step 1: Here we will Divide the given number into its prime factors.
Step 2: Form pairs of similar factors such that both factors in each pair are equal.
Step 3: Take one factor from the pair.
Step 4: Find the product of the factors obtained by taking one factor from each pair.
Step 5: That product is the square root of the given number.
Example: Find the square root of 144 by this method
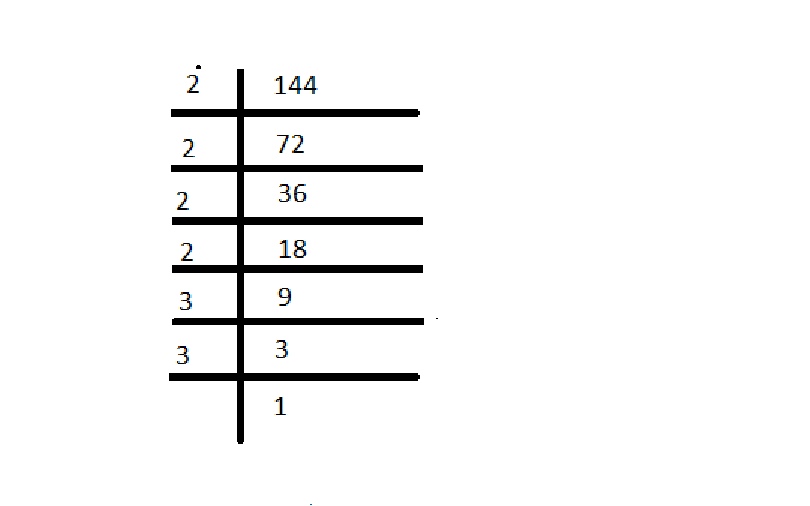
So, the Square root of 144 is 2 × 2 × 2 × 2 × 3 × 3
= 22 × 22 × 32
we can write as = (2 × 2 × 3)2
= (12)2
Perfect Square Root of 225

Here Square Root of 225 is
We can write as 5 × 5 × 3 × 3
= 52 × 32
= (5 × 3)2
= (15)2
Square Root by Estimation Method
Estimation and approximation refer to a reasonable guess of actual value to make calculations easier. This method also helps in estimating and approximating the square root of a given number.
Let’s use this method to find √15 and Find the nearest perfect square numbers to 15.
We know that 9 and 16 are the perfect square numbers that are nearest to 15. We also know that √16 = 4 and √9 = 3.
This also implies that √15 lies between both 3 and 4. Now, we need to see whether √15 is closer to 3 or 4.
Let us consider 3.5 and 4.
3.52 = 12.25 and 42 = 16. Hence √15 lies between 3.5 and 4 and closer to 4.
Now, we will find the squares of 3.8 and 3.9.
3.82 = 14.44 and 3.92 = 15.21.
This also implies that √15 lies between 3.8 and 3.9. We repeat the process and check between 3.85 and 3.9.
So we can observe that √15 = 3.872.
This is a very time-consuming process.
Square Root by Long Division Method
It is a method for dividing large numbers into steps or parts, breaking the division problem into a sequence of easier steps. With this method, we can find the exact square root of any given number.
First, we have to pair the number in two parts, for the digits before the decimal number, we pair from the right while for numbers after the decimal we pair from the right of the decimal.
So now here some examples of square root of 20.8849 and it gives us a perfect square root..

Find the square root correct up to 2 decimals 60.92
Using Long Division Method
Steps we have used here to calculate:
1) First we have to pair the number 60.92 in two parts
for the digits before the decimal number, we pair from right
while for numbers after the decimal we pair from the right of decimal….
So the square root of 60.92 is 7.805126 it doesn’t have a perfect square root….

Using Repeated subtraction Method
Solution:
60.92 – 1 = 59.92
59.92 – 3 = 56.92
56.92 – 5 = 51.92
51.92 – 7 = 44.92
44.92 – 9 = 35.92
35.92 – 11= 24.92
24.92 – 13 = 11.92
11.92 – 15 = – 4.92
From here its shows that by this method we will not get the 0 after continuing subtraction as result now coming in minus… so its shows that 60.92 doesn’t have a perfect square root… hence this method is not successful or you can say only successful for the numbers which have perfect square root…
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...