Find the root of given non decreasing function between A and B

Given three numbers a, b, and c that forms a monotonically increasing function 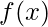of the form a*x² + b*x + c and two number A and B, the task is to find the root of the function i.e., find the value of x such that 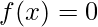where A ? x ? B.

Examples:

Input: a = 2, b = -3, c = -2, A = 0, B = 3 
Output: 2.0000 
Explanation:
f(x) = 2x^2 – 3x – 2 putting the value of x = 2.000 
We get f(2.000) = 2(2.000)^2 – 3(2.000) – 2 = 0
Input: a = 2, b = -3, c = -2, A = -2, B = 1 
Output: No solution

Approach: Below is the graphical representation of any function: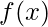

From the above graph, we have,

1. Whenever f(A)*f(B) ? 0, it means that the graph of the function will cut the x-axis somewhere within that range and signifies that somewhere there is a point which makes the value of the function as 0 and then the graph proceeds to be negative y-axis.
2. If f(A)*f(B) > 0, it means that in this range [A, B] the y values of f(A) and f(B) both remain positive throughout, so they never cut x-axis.

Therefore, from the above observation, the idea is to use Binary Search to solve this problem. Using the given range of [A, B] as lower and upper bound for the root of the equation, x can be found out by applying binary search on this range. Below are the steps:

1. Find the middle(say mid) of the range [A, B].
2. If f(mid)*f(A) ? 0 is true then search space is reduced to [A, mid], because the cut at x-axis has been occurred in this segment.
3. Else search space is reduced to [mid, B]
4. The minimum possible value for root is when the high value becomes just smaller than EPS(the smallest value ~10^-6) + lower bound value i.e., fabs(high – low) > EPS.
5. Print the value of the root.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
#define eps 1e-6

// Given function
double func(double a, double b,
            double c, double x)
{
    return a * x * x + b * x + c;
}

// Function to find the root of the
// given non-decreasing Function
double findRoot(double a, double b,
                double c, double low,
                double high)
{
    double x;

    // To get the minimum possible
    // answer for the root
    while (fabs(high - low) > eps) {

        // Find mid
        x = (low + high) / 2;

        // Search in [low, x]
        if (func(a, b, c, low)
                * func(a, b, c, x)
            <= 0) {
            high = x;
        }

        // Search in [x, high]
        else {
            low = x;
        }
    }

    // Return the required answer
    return x;
}

// Function to find the roots of the
// given equation within range [a, b]
void solve(double a, double b, double c,
        double A, double B)
{

    // If root doesn't exists
    if (func(a, b, c, A)
            * func(a, b, c, B)
        > 0) {
        cout << "No solution";
    }

    // Else find the root upto 4
    // decimal places
    else {
        cout << fixed
            << setprecision(4)
            << findRoot(a, b, c,
                        A, B);
    }
}

// Driver Code
int main()
{
    // Given range
    double a = 2, b = -3, c = -2,
        A = 0, B = 3;

    // Function Call
    solve(a, b, c, A, B);
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
import java.lang.*;

class GFG{

static final double eps = 1e-6;

// Given function
static double func(double a, double b,
                   double c, double x)
{
    return a * x * x + b * x + c;
}

// Function to find the root of the
// given non-decreasing Function
static double findRoot(double a, double b,
                       double c, double low,
                       double high)
{
    double x = -1;

    // To get the minimum possible
    // answer for the root
    while (Math.abs(high - low) > eps)
    {

        // Find mid
        x = (low + high) / 2;

        // Search in [low, x]
        if (func(a, b, c, low) *
            func(a, b, c, x) <= 0)
        {
            high = x;
        }

        // Search in [x, high]
        else
        {
            low = x;
        }
    }

    // Return the required answer
    return x;
}

// Function to find the roots of the
// given equation within range [a, b]
static void solve(double a, double b, double c,
                  double A, double B)
{

    // If root doesn't exists
    if (func(a, b, c, A) * func(a, b, c, B) > 0)
    {
        System.out.println("No solution");
    }

    // Else find the root upto 4
    // decimal places
    else
    {
        System.out.format("%.4f", findRoot(
            a, b, c, A, B));
    }
}

// Driver Code
public static void main (String[] args)
{

    // Given range
    double a = 2, b = -3, c = -2,
           A = 0, B = 3;

    // Function call
    solve(a, b, c, A, B);
}
}

// This code is contributed by offbeat

Python3

# Python3 program for the above approach
import math
eps = 1e-6

# Given function
def func(a ,b , c , x):

    return a * x * x + b * x + c

# Function to find the root of the
# given non-decreasing Function
def findRoot( a, b, c, low, high):

    x = -1

    # To get the minimum possible
    # answer for the root
    while abs(high - low) > eps:

        # Find mid
        x = (low + high) / 2

        # Search in [low, x]
        if (func(a, b, c, low) *
            func(a, b, c, x) <= 0):
            high = x

        # Search in [x, high]
        else:
            low = x

    # Return the required answer
    return x

# Function to find the roots of the
# given equation within range [a, b]
def solve(a, b, c, A, B):

    # If root doesn't exists
    if (func(a, b, c, A) *
        func(a, b, c, B) > 0):
        print("No solution")

    # Else find the root upto 4
    # decimal places
    else:
        print("{:.4f}".format(findRoot(
              a, b, c, A, B)))

# Driver code
if __name__ == '__main__':

    # Given range
    a = 2
    b = -3
    c = -2
    A = 0
    B = 3

    # Function call
    solve(a, b, c, A, B)

# This code is contributed by jana_sayantan

C#

// C# program for the above approach
using System;

class GFG{

static readonly double eps = 1e-6;

// Given function
static double func(double a, double b,
                   double c, double x)
{
    return a * x * x + b * x + c;
}

// Function to find the root of the
// given non-decreasing Function
static double findRoot(double a, double b,
                       double c, double low,
                       double high)
{
    double x = -1;

    // To get the minimum possible
    // answer for the root
    while (Math.Abs(high - low) > eps)
    {

        // Find mid
        x = (low + high) / 2;

        // Search in [low, x]
        if (func(a, b, c, low) *
            func(a, b, c, x) <= 0)
        {
            high = x;
        }

        // Search in [x, high]
        else
        {
            low = x;
        }
    }

    // Return the required answer
    return x;
}

// Function to find the roots of the
// given equation within range [a, b]
static void solve(double a, double b, double c,
                  double A, double B)
{

    // If root doesn't exists
    if (func(a, b, c, A) * func(a, b, c, B) > 0)
    {
        Console.WriteLine("No solution");
    }

    // Else find the root upto 4
    // decimal places
    else
    {
        Console.Write("{0:F4}", findRoot(
            a, b, c, A, B));
    }
}

// Driver Code
public static void Main(String[] args)
{

    // Given range
    double a = 2, b = -3, c = -2,
           A = 0, B = 3;

    // Function call
    solve(a, b, c, A, B);
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript program for the above approach

let eps = 1e-6;

// Given function
function func(a, b,
                   c, x)
{
    return a * x * x + b * x + c;
}

// Function to find the root of the
// given non-decreasing Function
function findRoot(a, b,
                       c, low,
                        high)
{
    let x = -1;

    // To get the minimum possible
    // answer for the root
    while (Math.abs(high - low) > eps)
    {

        // Find mid
        x = (low + high) / 2;

        // Search in [low, x]
        if (func(a, b, c, low) *
            func(a, b, c, x) <= 0)
        {
            high = x;
        }

        // Search in [x, high]
        else
        {
            low = x;
        }
    }

    // Return the required answer
    return x;
}

// Function to find the roots of the
// given equation within range [a, b]
function solve(a, b, c, A, B)
{

    // If root doesn't exists
    if (func(a, b, c, A) * func(a, b, c, B) > 0)
    {
        document.write("No solution");
    }

    // Else find the root upto 4
    // decimal places
    else
    {
        document.write(findRoot(
            a, b, c, A, B));
    }
}

// Driver Code

      // Given range
    let a = 2, b = -3, c = -2,
           A = 0, B = 3;

    // Function call
    solve(a, b, c, A, B);

</script>

Output:

2.0000

Time Complexity: O(log(B – A)) 
Auxiliary Space: O(1)