Find the remainder when N is divided by 4 using Bitwise AND operator
Last Updated :
10 Aug, 2023
Given a number N, the task is to find the remainder when N is divided by 4 using Bitwise AND operator.
Examples:
Input: N = 98
Output: 2
Explanation: 98 % 4 = 2. Hence the output is 2.
Input: 200
Output: 0
Explanation: 200 % 4 = 0. Hence output is 0.
Naive approach:
For solving the above-mentioned problem we can use a naïve method by using the Modulo (%) operator to find the remainder. But, the Modulo operator is computationally expensive and the method is inefficient.
C++
#include <iostream>
using namespace std;
int main() {
int N = 98;
int rem = N % 4;
cout << rem << endl;
return 0;
}
|
Java
class Main {
public static void main(String[] args) {
int N = 98;
int rem = N % 4;
System.out.println(rem);
}
}
|
Python3
def findRemainder(n: int) -> int:
return n % 4
n = 98
print(findRemainder(n))
|
C#
using System;
class Program
{
static void Main()
{
int N = 98;
int rem = N % 4;
Console.WriteLine(rem);
}
}
|
Javascript
function main() {
let N = 98;
let rem = N % 4;
console.log(rem);
}
main();
|
Efficient Approach:
If we carefully observe the binary representation of N and its remainder with 4, we observe that remainder is simply the rightmost two bits in N. To get the rightmost two bits in number N, we perform bitwise AND (&) with 3 because 3 in binary is 0011. To understand the approach better let us have a look at the image below:
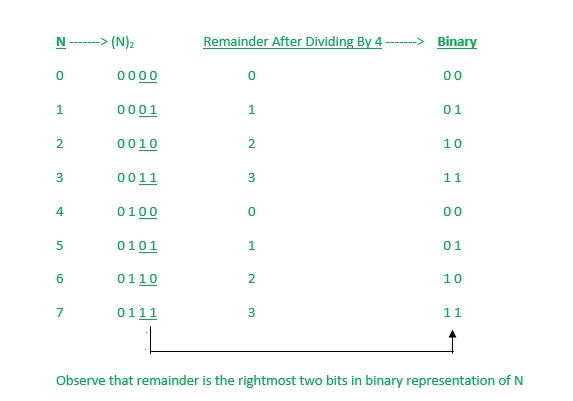
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findRemainder(int n)
{
int x = n & 3;
return x;
}
int main()
{
int N = 43;
int ans = findRemainder(N);
cout << ans << endl;
return 0;
}
|
C
#include <stdio.h>
int findRemainder(int n)
{
int x = n & 3;
return x;
}
int main()
{
int N = 43;
int ans = findRemainder(N);
printf("%d", ans);
return 0;
}
|
Java
class Main {
public static void main(String[] args)
{
int N = 43;
int ans = findRemainder(N);
System.out.println(ans);
}
public static int findRemainder(int n)
{
int x = n & 3;
return x;
}
}
|
Python 3
def findRemainder(n):
x = n & 3
return x
if __name__ == '__main__':
N = 43
ans = findRemainder(N)
print(ans)
|
C#
using System;
class GFG {
public static void Main()
{
int N = 43;
int ans = findRemainder(N);
Console.Write(ans);
}
public static int findRemainder(int n)
{
int x = n & 3;
return x;
}
}
# This code is contributed by chitranayal
|
Javascript
<script>
function findRemainder(n)
{
let x = n & 3;
return x;
}
let N = 43;
let ans = findRemainder(N);
document.write(ans);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Another Approach:
We can solve this problem using right shift operator (>>). The right shift operator shifts the bits of a number to the right by a specified number of positions. When we shift a number to the right by 2 positions (i.e., n >> 2), we effectively divide it by 4 and get the quotient as the result.
If we multiply the quotient by 4 and subtract it from the original number, we get the remainder. This can be expressed mathematically as:
N = 4 * (N >> 2) + (N & 3)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findRemainder(int n)
{
int quotient = n >> 2;
int remainder = n - (quotient << 2);
return remainder;
}
int main()
{
int N = 43;
int ans = findRemainder(N);
cout << ans << endl;
return 0;
}
|
C
#include<stdio.h>
int find_remainder(int n) {
int quotient = n >> 2;
int remainder = n - (quotient << 2);
return remainder;
}
int main() {
int N = 43;
int ans = find_remainder(N);
printf("%d\n", ans);
return 0;
}
|
Java
public class Main {
public static int findRemainder(int n)
{
int quotient = n >> 2;
int remainder = n - (quotient << 2);
return remainder;
}
public static void main(String[] args)
{
int N = 43;
int ans = findRemainder(N);
System.out.println(ans);
}
}
|
Python3
def find_remainder(n):
quotient = n >> 2
remainder = n - (quotient << 2)
return remainder
if __name__ == '__main__':
N = 43
ans = find_remainder(N)
print(ans)
|
C#
using System;
class Program {
static int FindRemainder(int n) {
int quotient = n >> 2;
int remainder = n - (quotient << 2);
return remainder;
}
static void Main(string[] args) {
int N = 43;
int ans = FindRemainder(N);
Console.WriteLine(ans);
}
}
|
Javascript
function findRemainder(n)
{
let quotient = n >> 2;
let remainder = n - (quotient << 2);
return remainder;
}
let N = 43;
let ans = findRemainder(N);
console.log(ans);
|
PHP
<?php
function find_remainder($n) {
$quotient = $n >> 2;
$remainder = $n - ($quotient << 2);
return $remainder;
}
$N = 43;
$ans = find_remainder($N);
echo $ans . "\n";
?>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Approach : Bitwise AND operator approach
Steps:
Calculate the last two bits of the given number by performing a Bitwise AND operation with 3 (11 in binary).
Return the result based on the following cases:
a. If the last two bits are 00, then the remainder is 0.
b. If the last two bits are 01, then the remainder is 1.
c. If the last two bits are 10, then the remainder is 2.
d. If the last two bits are 11, then the remainder is 3.
Here is the implementation of above approach:-
C++
#include <iostream>
using namespace std;
int remainderBy4(int n) {
int lastTwoBits = n & 3;
if (lastTwoBits == 0) {
return 0;
} else if (lastTwoBits == 1) {
return 1;
} else if (lastTwoBits == 2) {
return 2;
} else {
return 3;
}
}
int main() {
int n = 43;
cout << remainderBy4(n) << endl;
return 0;
}
|
Java
public class Main {
public static int remainderBy4(int n) {
int lastTwoBits = n & 3;
if (lastTwoBits == 0) {
return 0;
} else if (lastTwoBits == 1) {
return 1;
} else if (lastTwoBits == 2) {
return 2;
} else {
return 3;
}
}
public static void main(String[] args) {
int n = 43;
System.out.println(remainderBy4(n));
}
}
|
Python3
def remainderBy4(n: int) -> int:
lastTwoBits = n & 3
if lastTwoBits == 0:
return 0
elif lastTwoBits == 1:
return 1
elif lastTwoBits == 2:
return 2
else:
return 3
n = 43
print(remainderBy4(n))
|
C#
using System;
public class Program {
public static int RemainderBy4(int n) {
int lastTwoBits = n & 3;
if (lastTwoBits == 0) {
return 0;
} else if (lastTwoBits == 1) {
return 1;
} else if (lastTwoBits == 2) {
return 2;
} else {
return 3;
}
}
static void Main(string[] args) {
int n = 43;
Console.WriteLine(RemainderBy4(n));
}
}
|
Javascript
function remainderBy4(n) {
let lastTwoBits = n & 3;
if (lastTwoBits === 0) {
return 0;
} else if (lastTwoBits === 1) {
return 1;
} else if (lastTwoBits === 2) {
return 2;
} else {
return 3;
}
}
let n = 43;
console.log(remainderBy4(n));
|
Complexity:
Time Complexity: O(1) as we are only performing a single Bitwise AND operation and a few simple comparisons.
Auxiliary Space: O(1) as we are not using any extra data structure to store values.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...