Find the real and imaginary parts of the complex number z = e2 + 4i

A number refers to a word or symbol which represents a specific quantity. It is with the assistance of numbers only that multiple arithmetic operations are performed and that we are ready to develop a lot within the field of physics and arithmetic. One cannot live their life without the usage of numbers, even for the foremost basic chores or tasks. Even the cash exchanged for commodities may be a certain value represented by numbers. A bunch of numbers grouped together is employed to assign an individual as their contact number, such is that the prominence of numerals in our lives.

Types of numbers 

There are different types of numbers based on different characteristics and properties. Natural numbers, whole numbers, integers, rational numbers, irrational numbers, etc. Let’s take a look at their definitions,

• Natural Numbers: A group of numbers as is employed to count certain objects are called natural numbers. Such a group of numbers starts with 1(one) and goes on till infinity. It is to be noted that natural numbers include only positive integers.
• Whole Numbers: A group of numbers that has all the positive integers and 0.
• Integers: An integer is defined intrinsically as an entire number that will assume either positive, negative, or no value in the least.
• Rational Numbers: Such numbers can be expressed in the form of a fraction. These numbers have a terminating decimal expansion.
• Irrational Numbers: Such numbers can’t be expressed as a fraction.
• Real Numbers: Such numbers include both rational numbers and their irrational counterparts.

Real and Imaginary numbers

Such numbers which include both rational numbers and their irrational counterparts are called real numbers. They are based on the concept of a number line, with zero being the origin and all the numbers to its right, positive, and those in the left of the origin, negative.

Ofttimes it so happens while solving quadratic equations, that the discriminant comes out to be a negative value under the square root. This might sound impossible because by following the general rule in mathematics, the square of a negative number is a positive number so it does not make sense for a perfect square or any real number, for that matter, to be negative and under the root altogether. However, numbers can also be depicted as the square root of a negative number in mathematics. For example, 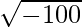 is an imaginary number, since it depicts the number 100, which is a perfect square as a negative number under a square root. Such numbers are not tangible, but still kind of real in the sense that they are used in mathematics. In other words, imaginary numbers are numbers that are the opposite of real numbers. They are not based on the concept of the number line, and as a result, cannot be depicted or plotted on one. Another way of defining an imaginary number could be such a number which yields a negative result when multiplied with itself, i.e., squared.

Representing an Imaginary Number Without the Square Root Part

An imaginary number, when written without using the root arithmetic expression can be written as a real number, multiplied by an iota, depicted i, which is an imaginary unit and iota (i) = √(-1).

Hence, 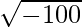 can be written as = 10√(-1) = 10i.

Powers of i

• i = √-1
• i² = -1
• i³ = i × i² = i × -1 = -i
• i⁴ = i² × i² = -1 × -1 = 1
• i⁵ = i × i⁴ = i
• i⁶ = i × i⁵ = i × i = i² = -1
• i⁷ = i × i⁶ = i × -1 = -i
• i⁸ = (i²)⁴ = (-1)⁴ = 1
• i⁹ = i × i⁸ = i × 1 = i
• i¹⁰ = i × i⁹ = i × i = i² = -1

Following this pattern, one can conclude that i repeats its values after every 4^th power.

Complex Numbers

A complex number can be called a hybrid of real and imaginary numbers, with the real number or constituent being any fraction, rational or irrational integer and its imaginary part being represented as a real number in multiplication with the imaginary unit iota, depicted i. Thus, a complex number shows a real number and an imaginary number combined by either of these two arithmetic operations, addition, and subtraction.

Standard Form of a Complex Number

A complex number, in its standard form, is expressed as a + ib, where a and b both are real numbers, but b being in multiplication with the imaginary variable i, represents the imaginary part of the whole complex number, which can be denoted by ‘z’. Hence, a complex number is usually written in the form z = a + ib, where a depicts the real part and ib or bi would be the imaginary constituent. For that matter, 0 + bi would also be regarded as a complex number with the real part being non-existent and bi depicting its imaginary counterpart.

Examples

• 5 + 2i is a complex number, where 5 is the real part and 2i depicts the imaginary part.
• e² + 12i  is a complex number, where e² is the real part and 12i is the imaginary part.
• √22 – 162i is a complex number, where √22 is the real part and 162i is the imaginary part.

Find the real and imaginary parts of the complex number z = e² + 4i.

Solution:

A complex number is usually written in the form z = a + ib, where a depicts the real part and ib or bi would be the imaginary constituent.

Hence, real part = e² and imaginary part = 4i.

Similar Problems

Question 1: Find the real and imaginary parts of e^-2 + i13.

Solution:

A complex number is usually written in the form z = a + ib, where a depicts the real part and ib or bi would be the imaginary constituent.

Real part = e^-2 = 1/ e² and imaginary part = 13i.

Question 2: Find the real and imaginary parts of e^z if z = x + iy.

Solution:

e^z = e^{x + iy}

= e^x(cosy + isiny)

= e^x cos y + e^x isiny

Hence the real part = e^x cos y and the imaginary part = e^x isiny.

Question 3: Find the real and imaginary parts of 3i²⁰ – i¹⁹.

Solution:

Clearly, i²⁰ = 1 and i¹⁹ = i.

So, the expression becomes 3(1) – i 

= 3 – i

Hence the real part = 3 and the imaginary part = 1.

Question 4: Find the real and imaginary parts of the number q if q ∈ R.

Solution:

q ∈ R, q is a real number, implying that it does not have any imaginary part. Alternatively one can say that the coefficient of i is zero.

Hence the real part and the imaginary part of q for all q ∈ R are q and zero respectively.

Question 5: Find the real and imaginary parts of 10i¹⁰⁰ + 2i⁹⁹.

Solution:

Clearly, i¹⁰⁰ = 1 and i⁹⁹ = -i

So, the expression becomes 10(1) + 2(-i)

= 10 – 2i

Hence the real part = 10 and the imaginary part = 2.