Find the ratio in which the point (– 1, 6) divides the line segment joining the points (– 3, 10) and (6, – 8)
Last Updated :
28 Jan, 2024
Geometry is undeniably one of the most important branches in the field of mathematics. Its significance is as profound as that of arithmetic and algebra, as much in our daily lives, as much as in the technicalities and intricacies of mathematics. Geometry, in daily lives, is basically prevalent everywhere. It is applied in designing a simple tiffin box to a mobile phone or a laptop to a water tank or even a bus, truck, and even dams. Hence anything which occupies space and has a definite shape has to be covered under the scope of geometry. In mathematical theory and problems too, the concept of geometry is employed to find the distance between two shapes, the space they take up, their sizes, and positions.
Coordinate Plane
Such a plane which is formed by the intersection of two lines, one of them being vertical and the other one horizontal, is called a co-ordinate plane in mathematics. It is a two- dimensional plane, with the vertical line being regarded as its y-axis and the horizontal one as the x-axis. The point of intersection of the two lines in the plane is called origin and is denoted by O. The figures on a matching grid are used to detect points. A coordinate plane can be used to graph points, lines, and much further. It acts as a chart and yields precise directions from one point to another.
Coordinates
Coordinates are a group of two values that locate a selected point on a coordinate plane grid, better referred to as a coordinate plane. A point inside a coordinate plane is known by its ordered pair (x, y), written in parentheses, like the X-coordinate and therefore the Y-coordinate. These coordinates are often positive, zero, or negative, depending on their position within the respective quadrants.
Signs of Coordinates in Different Quadrants
The coordinate plane gets divided into 4 quadrants with the x-axis and y-axis. The first quadrant is the uppermost right one where both the x and y coordinates are positive numbers; the second quadrant lies to the left of the first where the x coordinate is positive and the y coordinate is negative; the third quadrant lies directly below the second quadrant where the x coordinate is negative and the y coordinate is positive; the fourth quadrant lies directly below the first quadrant and to the right of the third quadrant where both the x and y coordinates are negative.

Section Formula
In cartesian system, a given line segment would pass through infinite number of points. It is obvious that all such points divide the given line segment into two parts which may or may not be equal in length. Now if the coordinates of such a point are known, the it is possible to find out the ratio in which the division of the line segment took place. The reverse of this situation is also possible, given the ratio in which the line segment gets divided, one can calculate the coordinates of the point responsible for such division. This is when the concept of section formula comes into picture.
Section formula is used to determine the coordinate of a point that divides a line segment joining two points into two parts such that the ratio of their length is m:n.
Suppose A(a1, b1) and B(a2, b2) be the two points in the xy- plane and T be the point dividing the line segment AB internally in the ratio m:n, then the section formula for determining the coordinates of point T is given by:
T(a, b) = 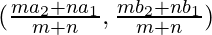
Find the ratio in which the point (– 1, 6) divides the line segment joining the points (– 3, 10) and (6, – 8).
Solution:
Let the ratio in which the point T(-1, 6) divides the line segment joining A(– 3, 10) and B(6, – 8) be m:n.
As per section formula, coordinates of point T are given by:
(-1, 6) = 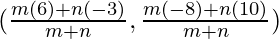
⇒ -1 =  and 6 =
and 6 = 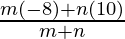
⇒ −m − n = 6m − 3n and 6m + 6n = −8m + 10n
⇒ 2n = 7m and 4n = 14m
⇒ 7m = 2n
⇒ m:n = 2:7
Hence the point (– 1, 6) divides the line segment joining the points (– 3, 10) and (6, – 8) internally in the ratio 2:7.
Similar Problems
Question 1. Find the ratio in which the point (– 7/5,0) divides the line segment joining the points (4, 6) and (−5, – 4).
Solution:
Let the ratio in which the point T(– 7/5,0) divides the line segment joining A(4, 6) and B(−5, – 4) be m:n.
As per section formula, coordinates of point T are given by:
(– 7/5,0) = 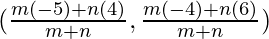
⇒ -7/5 =  and 0 =
and 0 = 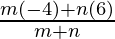
⇒ −7m − 7n = -25m + 20n and 0 = −4m + 6n
⇒ 27n = 18m and 6n = 4m
⇒ 2m = 3n
⇒ m:n = 3:2
Hence the point (– 7/5,0) divides the line segment joining the points (4, 6) and (−5, – 4) internally in the ratio 3:2.
Question 2. Find the ratio in which the point (0, 3) divides the line segment joining the points (2, 1) and (-3, 6).
Solution:
Let the ratio in which the point T(0, 3) divides the line segment joining A(2, 1) and B(-3, 6) be m:n.
As per section formula, coordinates of point T are given by:
(0, 3) = 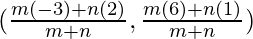
⇒ 0 =  and 3 =
and 3 = 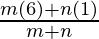
⇒ 0 = -3m + 2n and 3m + 3n = 6m + n
⇒ 2n = 3m and 6n = 4m
⇒ 3m = 2n
⇒ m:n = 2:3
Hence the point (0, 3) divides the line segment joining the points (2, 1) and (−3, 6) internally in the ratio 2:3.
Question 3. Find the ratio in which the point (3, 6) divides the line segment joining the points (4, 8) and (2, 4).
Solution:
Let the ratio in which the point T(3, 6) divides the line segment joining A(4, 8) and B(2, 4) be m:n.
As per section formula, coordinates of point T are given by:
(3, 6) = 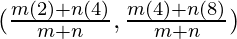
⇒ 3 =  and 6 =
and 6 = 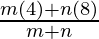
⇒ 3m + 3n = 2m + 4n and 6m + 6n = 4m + 8n
⇒ n = m and 2n = 2m
⇒ m = n
⇒ m:n = 1:1
Hence the point (3, 6) divides the line segment joining the points (4, 8) and (2, 4) internally in the ratio 1:1.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...