Find the position of given element N in infinite spiral matrix starting from top-left
Last Updated :
07 Aug, 2022
Given a number N and an infinite 2D matrix, which is to be filled using the algorithm given below, the task is to find the coordinates of the given element present in the matrix. The algorithm is as follows:
- The leftmost and topmost cell of the matrix is filled with 1. Then, all the cells are filled with consecutive numbers starting from 2
- The leftmost non-filled cell in the first row is filled. Then, while the left neighbor of the last filled cell is filled, the cells below it are filled next, until the last filled cell has a non-filled left neighbor
- Next, the cells are filled from right to the left until the first column. Then, again the leftmost non-filled cell in the first row is filled
- The above two steps are repeated infinitely
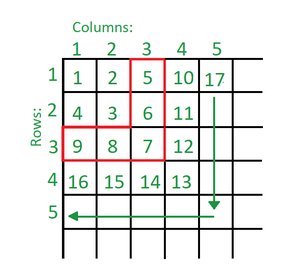
Examples:
Input: N = 12
Output: 3 4
Explanation: 12 lies in the cell with row as 3 and column as 4
Input: N = 10549857
Output: 353 3249
Explanation: 10549857 lies in the cell with row as 353 and column as 3249
Approach: Following observations can be made:
- In the above image that the red highlighted portion or ‘inverted L’ formed by the 3rd row and 3rd column consists of all numbers greater than 4 and smaller than 10. Similarly, the ‘inverted L’ formed by the 4th row and 4th column consists of numbers greater than 9 and smaller than 17
- In other words, numbers present are excluding the current perfect square till including the next perfect square
- To find the ‘inverted L’ in which the number lies, find the ceil of the square root of the number
- The difference between the square of ‘inverted L’ and the given number is calculated, say d
- If l is the ‘inverted L’ in which the number lies and n denotes the given number, then:
d = l^2 – N
- If this difference d is less than n, then the row r and column c of n is given by:
r = l
c = d + l
- If this difference d is greater than or equal to n, then the row r and column c of n is given by:
r = 2l – d – 1
c = l
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findCoordinates(int n)
{
int r, c;
int l = ceil(sqrt(n));
int d = (l * l) - n;
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
cout << r << " " << c;
}
int main()
{
int N = 10549857;
findCoordinates(N);
return 0;
}
|
Java
public class GFG {
static void findCoordinates(int n)
{
int r, c;
int l = (int)Math.ceil(Math.sqrt(n));
int d = (l * l) - n;
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
System.out.print(r + " " + c);
}
public static void main (String[] args) {
int N = 10549857;
findCoordinates(N);
}
}
|
Python3
import math
def findCoordinates(n):
l = math.ceil(math.sqrt(n))
d = (l * l) - n
if (d < l):
r = l
c = d + 1
else:
c = l
r = (2 * l) - d - 1
print(f"{r} {c}")
N = 10549857
findCoordinates(N)
|
C#
using System;
public class GFG {
static void findCoordinates(int n)
{
int r, c;
int l = (int)Math.Ceiling(Math.Sqrt(n));
int d = (l * l) - n;
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
Console.Write(r + " " + c);
}
public static void Main (string[] args) {
int N = 10549857;
findCoordinates(N);
}
}
|
Javascript
<script>
function findCoordinates(n) {
let r, c;
let l = Math.ceil(Math.sqrt(n));
let d = (l * l) - n;
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
document.write(r + " " + c);
}
let N = 10549857;
findCoordinates(N);
</script>
|
Time Complexity: O(log(n)) because inbuilt sqrt function has been used
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...