Find the number of words of X vowels and Y consonants that can be formed from M vowels and N consonants
Last Updated :
21 Jun, 2022
Given four integers X, Y, M and N. The task is to find the number of ways to form a word by choosing X number of vowels and Y number of consonants from total numbers of M vowels and N consonants.
Examples:
Input : X = 2, Y = 2, M = 3, N = 3
Output : 216
The total number of ways of choosing 2 vowels from a total number of 3 vowels is 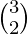 i.e 3
i.e 3
The total number of ways of choosing 2 consonants from a total number of 3 consonants is 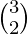 i.e 3.
i.e 3.
The total number of ways of selecting 2 consonants from 3 and 2 vowels from 3 is 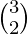 *
* 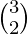 = 9
= 9
The total number of ways of arranging 4 letters among themselves = 4! = 24
Hence, the required number of ways = 24 * 9 = 216
Input : X = 1, Y = 2, M = 2, N = 3
Output : 36
Recommended: Please try your approach on {IDE} first, before moving on to the solution.
Approach :
- The total number of ways of choosing X vowels from a total number of M vowels is
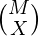
- The total number of ways of choosing Y consonants from a total number of N consonants is
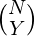
- The total number of ways of selecting Y consonants from N and X vowels from M is
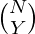 *
* 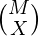
- The total number of ways of arranging (X+Y) letters among themselves = (X+Y)!
- Hence, the required number of ways = (X+Y)! *
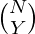 *
* 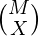
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int fact(int n)
{
int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
int nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
int NumberOfWays(int X, int Y, int M, int N)
{
return fact(X + Y) * nCr(M, X) * nCr(N, Y);
}
int main()
{
int X = 2, Y = 2, M = 3, N = 3;
cout << NumberOfWays(X, Y, M, N);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG
{
static int fact(int n)
{
int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
static int nCr(int n, int r)
{
return fact(n) / (fact(r) *
fact(n - r));
}
static int NumberOfWays(int X, int Y,
int M, int N)
{
return fact(X + Y) * nCr(M, X) *
nCr(N, Y);
}
public static void main (String[] args)
throws java.lang.Exception
{
int X = 2, Y = 2, M = 3, N = 3;
System.out.println(NumberOfWays(X, Y, M, N));
}
}
|
Python3
def fact(n):
res = 1
for i in range(2, n + 1, 1):
res = res * i
return res
def nCr(n, r):
return fact(n) // (fact(r) * fact(n - r))
def NumberOfWays(X, Y, M, N):
return fact(X + Y) * nCr(M, X) * nCr(N, Y)
if __name__ == '__main__':
X = 2
Y = 2
M = 3
N = 3
print(NumberOfWays(X, Y, M, N))
|
C#
using System;
class GFG
{
static int fact(int n)
{
int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
static int nCr(int n, int r)
{
return fact(n) / (fact(r) *
fact(n - r));
}
static int NumberOfWays(int X, int Y,
int M, int N)
{
return fact(X + Y) * nCr(M, X) *
nCr(N, Y);
}
public static void Main (String[] args)
{
int X = 2, Y = 2, M = 3, N = 3;
Console.WriteLine(NumberOfWays(X, Y, M, N));
}
}
|
Javascript
<script>
function fact(n) {
var res = 1;
for (var i = 2; i <= n; i++)
res = res * i;
return res;
}
function nCr(n, r) {
return fact(n) / (fact(r) * fact(n - r));
}
function NumberOfWays(X, Y, M, N) {
return fact(X + Y) * nCr(M, X) * nCr(N, Y);
}
var X = 2,
Y = 2,
M = 3,
N = 3;
document.write(NumberOfWays(X, Y, M, N));
</script>
|
Time Complexity: O(n), time to calculate factorial of n
Auxiliary Space: O(1), as no extra space is required
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...