Find the number of primitive roots modulo prime
Last Updated :
29 Jun, 2022
Given a prime 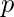 . The task is to count all the primitive roots of
. The task is to count all the primitive roots of 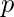 .
.
A primitive root is an integer x (1 <= x < p) such that none of the integers x – 1, x2 – 1, …., xp – 2 – 1 are divisible by 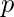 but xp – 1 – 1 is divisible by
but xp – 1 – 1 is divisible by 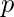 .
.
Examples:
Input: P = 3
Output: 1
The only primitive root modulo 3 is 2.
Input: P = 5
Output: 2
Primitive roots modulo 5 are 2 and 3.
Approach: There is always at least one primitive root for all primes. So, using Eulers totient function we can say that f(p-1) is the required answer where f(n) is euler totient function.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countPrimitiveRoots(int p)
{
int result = 1;
for (int i = 2; i < p; i++)
if (__gcd(i, p) == 1)
result++;
return result;
}
int main()
{
int p = 5;
cout << countPrimitiveRoots(p - 1);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int __gcd(int a, int b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a-b, b);
return __gcd(a, b-a);
}
static int countPrimitiveRoots(int p)
{
int result = 1;
for (int i = 2; i < p; i++)
if (__gcd(i, p) == 1)
result++;
return result;
}
public static void main (String[] args) {
int p = 5;
System.out.println( countPrimitiveRoots(p - 1));
}
}
|
Python3
from math import gcd
def countPrimitiveRoots(p):
result = 1
for i in range(2, p, 1):
if (gcd(i, p) == 1):
result += 1
return result
if __name__ == '__main__':
p = 5
print(countPrimitiveRoots(p - 1))
|
C#
using System;
class GFG {
static int __gcd(int a, int b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a-b, b);
return __gcd(a, b-a);
}
static int countPrimitiveRoots(int p)
{
int result = 1;
for (int i = 2; i < p; i++)
if (__gcd(i, p) == 1)
result++;
return result;
}
static public void Main (String []args) {
int p = 5;
Console.WriteLine( countPrimitiveRoots(p - 1));
}
}
|
PHP
<?php
function __gcd($a, $b)
{
if ($a == 0)
return b;
if ($b == 0)
return $a;
if ($a == $b)
return $a;
if ($a > $b)
return __gcd($a - $b, $b);
return __gcd($a, $b - $a);
}
function countPrimitiveRoots($p)
{
$result = 1;
for ($i = 2; $i < $p; $i++)
if (__gcd($i, $p) == 1)
$result++;
return $result;
}
$p = 5;
echo countPrimitiveRoots($p - 1);
?>
|
Javascript
<script>
function __gcd( a, b)
{
if (a == 0)
return b;
if (b == 0)
return a;
if (a == b)
return a;
if (a > b)
return __gcd(a-b, b);
return __gcd(a, b-a);
}
function countPrimitiveRoots(p)
{
var result = 1;
for (var i = 2; i < p; i++)
if (__gcd(i, p) == 1)
result++;
return result;
}
var p = 5;
document.write( countPrimitiveRoots(p - 1));
</script>
|
Time Complexity: O(p * log(min(a, b))), where a and b are two parameters of gcd.
Auxiliary Space: O(log(min(a, b)))
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...