Find the Nth term of the series 2, 15, 41, 80, 132…

Given a number N, the task is to find the Nth term of the series 2, 15, 41, 80, 132….
Examples:

Input: N = 2 
Output: 15
Input: N = 5 
Output: 132 

Approach: From the given series, the formula for Nth term can be found as: 

1st term = 2
2nd term = 2 + 1 * 13 = 15
3rd term = 15 + 2 * 13 = 41
4th term = 41 + 3 * 13 = 80
.
.
Nth term = (N - 1)th term
         + (N - 1) * 13

Therefore, the Nth term of the series is given as 

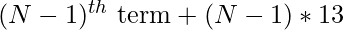
Below are the steps to find the Nth term using recursion:
Recursively iterate from value N: 

• Base case: If the value called recursively is 1, then it is the first term of the series. Therefore return 2 from the function. 
  

if(N == 1) 
  return 2;

• Recursive call: If the base case is not met, then recursively iterate from the function according to the Nth term of the series: 
  

(N - 1) * 13 + func(N - 1);

• Return statement: At each recursive call(except the base case), return the recursive function for next iteration. 
  

return ((13 * (N - 1))
       + func(N, i + 1));

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Recursive function to find Nth term
int nthTerm(int N)
{
    // Base Case
    if (N == 1) {
        return 2;
    }

    // Recursive Call according to
    // Nth term of the series
    return ((N - 1) * 13)
           + nthTerm(N - 1);
}

// Driver Code
int main()
{
    // Input Nth term
    int N = 17;

    // Function call
    cout << nthTerm(N) << endl;
    return 0;
}

Java

// Java program for the above approach

class GFG{

// Recursive function to find Nth term
static int nthTerm(int N)
{
    // Base Case
    if (N == 1)
    {
        return 2;
    }

    // Recursive Call according to
    // Nth term of the series
    return ((N - 1) * 13) +
            nthTerm(N - 1);
}

// Driver Code
public static void main(String[] args)
{
    // Input Nth term
    int N = 17;

    // Function call
    System.out.print(nthTerm(N) + "\n");
}
}

// This code is contributed by 29AjayKumar

Python 3

# Python 3 program for the above approach

# Recursive function to find Nth term
def nthTerm(N):

    # Base Case
    if (N == 1):
        return 2

    # Recursive Call according to
    # Nth term of the series
    return ((N - 1) * 13) + nthTerm(N - 1)

# Driver Code
if __name__ == '__main__':

    # Input Nth term
    N = 17

    # Function call
    print(nthTerm(N))

# This code is contributed by Bhupendra_Singh

C#

// C# program for the above approach
using System;

public class GFG{

// Recursive function to find Nth term
static public int nthTerm(int N)
{
    // Base Case
    if (N == 1)
    {
        return 2;
    }

    // Recursive Call according to
    // Nth term of the series
    return ((N - 1) * 13) + nthTerm(N - 1);
}

// Driver Code
static public void Main ()
{
    // Input Nth term
    int N = 17;

    // Function call
    Console.WriteLine(nthTerm(N));
}
}

//This code is contributed by shubhamsingh10

Javascript

<script>
// javascript program for the above approach

// Recursive function to find Nth term
function nthTerm( N)
{

    // Base Case
    if (N == 1) {
        return 2;
    }

    // Recursive Call according to
    // Nth term of the series
    return ((N - 1) * 13)
           + nthTerm(N - 1);
}

// Driver Code

    // Input Nth term
    let N = 17;

    // Function call
   document.write( nthTerm(N) );

// This code is contributed by Rajput-Ji

</script>

Output

1770

Time Complexity: O(N) for given input N

Auxiliary Space: O(N) for implicit call stack

Dynamic Programming (Top Down Using Memoization):

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

int static dp[1001];

// function to find Nth term
int nthTerm(int N)
{
    // Base Case
    if (N == 1) {
        return 2;
    }

    // If a value already present,
    // return it
    if(dp[N] != -1) {
        return dp[N];
    }
    // Recursive Call according to
    // Nth term of the series and
    // store it in dp
    dp[N] = ((N - 1) * 13) + nthTerm(N - 1);

    // Return dp
    return dp[N];
}

// Driver Code
int main()
{
    // Input Nth term
    int N = 17;

    memset(dp, -1, sizeof(dp));

    // Function call
    cout << nthTerm(N) << endl;
    return 0;
}
// This code is contributed by Samim Hossain Mondal.

Java

// Java implementation of above approach
import java.util.*;
public class GFG{

  static int []dp = new int[1001];

  // function to find Nth term
  static int nthTerm(int N)
  {
    // Base Case
    if (N == 1) {
      return 2;
    }

    // If a value already present,
    // return it
    if(dp[N] != -1) {
      return dp[N];
    }
    // Recursive Call according to
    // Nth term of the series and
    // store it in dp
    dp[N] = ((N - 1) * 13) + nthTerm(N - 1);

    // Return dp
    return dp[N];
  }

  // Driver code
  public static void main(String []args)
  {
    // Input Nth term
    int N = 17;

    for(int i = 0; i < 1001; i++) {
      dp[i] = -1;
    }

    System.out.println(nthTerm(N));
  }
}

// This code is contributed by Samim Hossain Mondal.

Python

# Pythonnprogram for the above approach

# Taking the matrix as globally
dp = [-1 for i in range(1001)]

# Function to find Nth term
def nthTerm(N):

    # Base Case
    if (N == 1):
        return 2

    # If a value already present,
    # return it
    if(dp[N] != -1):
        return dp[N]

    # Recursive Call according to
    # Nth term of the series and
    # store it in dp
    dp[N] = ((N - 1) * 13) + nthTerm(N - 1)

    # Return dp
    return dp[N]

# Driver Code
if __name__ == '__main__':

    # Input Nth term
    N = 17

    # Function call
    print(nthTerm(N))

# This code is contributed by Samim Hossain Mondal.

C#

// C# implementation of above approach
using System;
class GFG
{
  static int []dp = new int[1001];

  // function to find Nth term
  static int nthTerm(int N)
  {

    // Base Case
    if (N == 1) {
      return 2;
    }

    // If a value already present,
    // return it
    if(dp[N] != -1) {
      return dp[N];
    }

    // Recursive Call according to
    // Nth term of the series and
    // store it in dp
    dp[N] = ((N - 1) * 13) + nthTerm(N - 1);

    // Return dp
    return dp[N];
  }

  // Driver code
  public static void Main()
  {

    // Input Nth term
    int N = 17;

    for(int i = 0; i < 1001; i++) {
      dp[i] = -1;
    }

    Console.Write(nthTerm(N));
  }
}

// This code is contributed by Samim Hossain Mondal.

Javascript

<script>
// Javascript program for the above approach

let dp = [];

// function to find Nth term
function nthTerm(N)
{
    // Base Case
    if (N == 1) {
        return 2;
    }

    // If a value already present,
    // return it
    if(dp[N] != -1) {
        return dp[N];
    }
    // Recursive Call according to
    // Nth term of the series and
    // store it in dp
    dp[N] = ((N - 1) * 13) + nthTerm(N - 1);

    // Return dp
    return dp[N];
}

// Driver Code

// Input Nth term
let N = 17;

for(let i = 0; i < 1001; i++) {
    dp[i] = -1;
}

// Function call
document.write(nthTerm(N));

// This code is contributed by Samim Hossain Mondal.
</script>

Output

1770

Time Complexity: O(N)

Auxiliary Space: O(1001)