Find the node with maximum value in a Binary Search Tree
Given a Binary Search Tree, the task is to find the node with the maximum value in a BST.
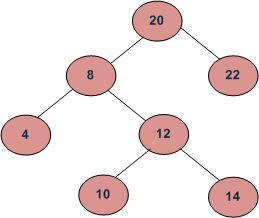
For the above tree, we start with 20, then we move right to 22. We keep on moving to the right until we see NULL. Since the right of 22 is NULL, 22 is the node with the maximum value.
Approach: This is quite simple. Just traverse the node from root to right recursively until the right is NULL. The node whose right is NULL is the node with the maximum value.
C++
#include <bits/stdc++.h>using namespace std; /* A binary tree node has data, pointer to left child and a pointer to right child */struct node { int data; struct node* left; struct node* right;}; // Function to create a new nodestruct node* newNode(int data){ struct node* newnode = new node(); newnode->data = data; newnode->left = NULL; newnode->right = NULL; return (newnode);} // Function to insert a new node in BSTstruct node* insert(struct node* node, int data){ /* 1. If the tree is empty, return a new, single node */ if (node == NULL) return (newNode(data)); else { /* 2. Otherwise, recur down the tree */ if (data <= node->data) node->left = insert(node->left, data); else node->right = insert(node->right, data); /* return the (unchanged) node pointer */ return node; }} // Function to find the node with maximum value// i.e. rightmost leaf nodeint maxValue(struct node* node){ /* loop down to find the rightmost leaf */ struct node* current = node; while (current->right != NULL) current = current->right; return (current->data);} // Driver codeint main(){ struct node* root = NULL; root = insert(root, 4); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 6); insert(root, 5); cout << "Maximum value in BST is " << maxValue(root); return 0;} |
Java
// Java implementation to find the sum of last// 'n' nodes of the Linked Listimport java.util.*; class GFG{ /* A binary tree node has data, pointer to left child and a pointer to right child */static class node{ int data; node left; node right;}; // Function to create a new nodestatic node newNode(int data){ node node = new node(); node.data = data; node.left = null; node.right = null; return (node);} // Function to insert a new node in BSTstatic node insert(node node, int data){ /* 1. If the tree is empty, return a new, single node */ if (node == null) return (newNode(data)); else { /* 2. Otherwise, recur down the tree */ if (data <= node.data) node.left = insert(node.left, data); else node.right = insert(node.right, data); /* return the (unchanged) node pointer */ return node; }} // Function to find the node with maximum value// i.e. rightmost leaf nodestatic int maxValue(node node){ /* loop down to find the rightmost leaf */ node current = node; while (current.right != null) current = current.right; return (current.data);} // Driver codepublic static void main(String[] args) { node root = null; root = insert(root, 4); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 6); insert(root, 5); System.out.println("Maximum value in BST is " + maxValue(root));}} /* This code is contributed by PrinciRaj1992 */ |
Python3
import sysimport math # A binary tree node has data, pointer to left child # and a pointer to right child class Node: def __init__(self,data): self.data = data self.left = None self.right = None # Function to insert a new node in BSTdef insert(root, data): # 1. If the tree is empty, return a new, # single node if not root: return Node(data) # 2. Otherwise, recur down the tree if data < root.data: root.left = insert(root.left, data) if data > root.data: root.right = insert(root.right, data) # return the (unchanged) node pointer return root # Function to find the node with maximum value # i.e. rightmost leaf node def maxValue(root): current = root #loop down to find the rightmost leaf while(current.right): current = current.right return current.data # Driver code if __name__=='__main__': root=None root = insert(root,2) root = insert(root,1) root = insert(root,3) root = insert(root,6) root = insert(root,5) print("Maximum value in BST is {}".format(maxValue(root))) # This code is contributed by Vikash Kumar 37 |
C#
// C# implementation to find the sum of last // 'n' nodes of the Linked List using System; class GFG { /* A binary tree node has data, pointer to left child and a pointer to right child */public class node { public int data; public node left; public node right; }; // Function to create a new node static node newNode(int data) { node node = new node(); node.data = data; node.left = null; node.right = null; return (node); } // Function to insert a new node in BST static node insert(node node, int data) { /* 1. If the tree is empty, return a new, single node */ if (node == null) return (newNode(data)); else { /* 2. Otherwise, recur down the tree */ if (data <= node.data) node.left = insert(node.left, data); else node.right = insert(node.right, data); /* return the (unchanged) node pointer */ return node; } } // Function to find the node with maximum value // i.e. rightmost leaf node static int maxValue(node node) { /* loop down to find the rightmost leaf */ node current = node; while (current.right != null) current = current.right; return (current.data); } // Driver code public static void Main(String[] args) { node root = null; root = insert(root, 4); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 6); insert(root, 5); Console.WriteLine("Maximum value in BST is " + maxValue(root)); } } // This code is contributed by Rajput-Ji |
Javascript
<script> // javascript implementation to find the sum of last // 'n' nodes of the Linked List /* * A binary tree node has data, pointer to left child and a pointer to right * child */ class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Function to create a new node function newNode(data) { var node = new Node(); node.data = data; node.left = null; node.right = null; return (node); } // Function to insert a new node in BST function insert( node , data) { /* * 1. If the tree is empty, return a new, single node */ if (node == null) return (newNode(data)); else { /* 2. Otherwise, recur down the tree */ if (data <= node.data) node.left = insert(node.left, data); else node.right = insert(node.right, data); /* return the (unchanged) node pointer */ return node; } } // Function to find the node with maximum value // i.e. rightmost leaf node function maxValue( node) { /* loop down to find the rightmost leaf */ var current = node; while (current.right != null) current = current.right; return (current.data); } // Driver code var root = null; root = insert(root, 4); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 6); insert(root, 5); document.write("Maximum value in BST is " + maxValue(root)); // This code contributed by Rajput-Ji </script> |
Output:
Maximum value in BST is 6
Time Complexity: O(N)
Auxiliary Space: O(1)
Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.
In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.
