Find the node whose xor with x gives maximum value

Given a tree, and the weights of all the nodes and an integer x, the task is to find a node i such that weight[i] xor x is maximum.
Examples:

Input:

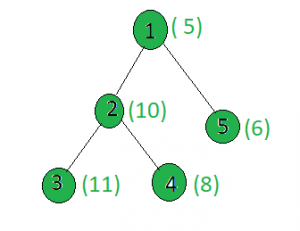
x = 15 
Output: 1 
Node 1: 5 xor 15 = 10 
Node 2: 10 xor 15 = 5 
Node 3: 11 xor 15 = 4 
Node 4: 8 xor 15 = 7 
Node 5: 6 xor 15 = 9 

Approach: Perform dfs on the tree and keep track of the node whose weighted xor with x gives the maximum value.
Below is the implementation of the above approach: 

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;

int maximum = INT_MIN, x, ans;

vector<int> graph[100];
vector<int> weight(100);

// Function to perform dfs to find
// the maximum xored value
void dfs(int node, int parent)
{
    // If current value is less than
    // the current maximum
    if (maximum < (weight[node] ^ x)) {
        maximum = weight[node] ^ x;
        ans = node;
    }
    for (int to : graph[node]) {
        if (to == parent)
            continue;
        dfs(to, node);
    }
}

// Driver code
int main()
{
    x = 15;

    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;

    // Edges of the tree
    graph[1].push_back(2);
    graph[2].push_back(3);
    graph[2].push_back(4);
    graph[1].push_back(5);

    dfs(1, 1);

    cout << ans;

    return 0;
}

Java

// Java implementation of the approach
import java.util.*;

class GFG
{

    static int maximum = Integer.MIN_VALUE, x, ans;

    @SuppressWarnings("unchecked")
    static Vector<Integer>[] graph = new Vector[100];
    static int[] weight = new int[100];

    // This block is executed even before main() function
    // This is necessary otherwise this program will
    // throw "NullPointerException"
    static
    {
        for (int i = 0; i < 100; i++)
            graph[i] = new Vector<>();
    }

    // Function to perform dfs to find
    // the maximum xored value
    static void dfs(int node, int parent)
    {

        // If current value is less than
        // the current maximum
        if (maximum < (weight[node] ^ x))
        {
            maximum = weight[node] ^ x;
            ans = node;
        }
        for (int to : graph[node])
        {
            if (to == parent)
                continue;
            dfs(to, node);
        }
    }

    // Driver Code
    public static void main(String[] args)
    {
        x = 15;

        // Weights of the node
        weight[1] = 5;
        weight[2] = 10;
        weight[3] = 11;
        weight[4] = 8;
        weight[5] = 6;

        // Edges of the tree
        graph[1].add(2);
        graph[2].add(3);
        graph[2].add(4);
        graph[1].add(5);

        dfs(1, 1);

        System.out.println(ans);
    }
}

// This code is contributed by
// sanjeev2552

Python3

# Python3 implementation of the approach
import sys
maximum = -sys.maxsize - 1
graph = [[0 for i in range(100)]
            for j in range(100)]
weight = [0 for i in range(100)]
ans = []

# Function to perform dfs to find
# the maximum xored value
def dfs(node, parent):
    global maximum

    # If current value is less than
    # the current maximum
    if (maximum < (weight[node] ^ x)):
        maximum = weight[node] ^ x
        ans.append(node)

    for to in graph[node]:
        if (to == parent):
            continue
        dfs(to, node)

# Driver code
if __name__ == '__main__':
    x = 15

    # Weights of the node
    weight[1] = 5
    weight[2] = 10
    weight[3] = 11
    weight[4] = 8
    weight[5] = 6

    # Edges of the tree
    graph[1].append(2)
    graph[2].append(3)
    graph[2].append(4)
    graph[1].append(5)

    dfs(1, 1)

    print(ans[0])

# This code is contributed by
# Surendra_Gangwar

C#

// C# implementation of the approach
using System;
using System.Collections.Generic;

class GFG
{

static int maximum = int.MinValue, x,
ans = int.MaxValue;

static List<List<int>> graph = new List<List<int>>();
static List<int> weight = new List<int>();


// Function to perform dfs to find
// the maximum value
static void dfs(int node, int parent)
{
    // If current value is less than
    // the current maximum
    if (maximum < (weight[node] ^ x))
    {
        maximum = weight[node] ^ x;
        ans = node;
    }

    for (int i = 0; i < graph[node].Count; i++)
    {
        if (graph[node][i] == parent)
            continue;
        dfs(graph[node][i], node);
    }
}

// Driver code
public static void Main()
{
    x = 15;

    // Weights of the node
    weight.Add(0);
    weight.Add(5);
    weight.Add(10);
    weight.Add(11);;
    weight.Add(8);
    weight.Add(6);

    for(int i = 0; i < 100; i++)
    graph.Add(new List<int>());

    // Edges of the tree
    graph[1].Add(2);
    graph[2].Add(3);
    graph[2].Add(4);
    graph[1].Add(5);

    dfs(1, 1);
    Console.Write( ans);
}
}

// This code is contributed by SHUBHAMSINGH10

Javascript

<script>
// Javascript implementation of the approach


let maximum = Number.MIN_SAFE_INTEGER;
let ans = [];

let graph = new Array();

for(let i = 0; i < 100; i++){
    graph.push(new Array().fill(0));
}

let weight = new Array(100).fill(0);


// Function to perform dfs to find
// the maximum xored value
function dfs(node, parent) {
    // If current value is less than
    // the current maximum
    if (maximum < (weight[node] ^ x)) {
        maximum = weight[node] ^ x;
        ans = node;
    }
    for (let to of graph[node]) {
        if (to == parent)
            continue;
        dfs(to, node);
    }
}

// Driver code

let x = 15;

// Weights of the node
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;

// Edges of the tree
graph[1].push(2);
graph[2].push(3);
graph[2].push(4);
graph[1].push(5);

dfs(1, 1);

document.write(ans);

// This code is contributed by gfgking
</script>

Output:

1

Complexity Analysis:

• Time Complexity : O(N). 
  In dfs, every node of the tree is processed once and hence the complexity due to the dfs is O(N) if there are total N nodes in the tree. Therefore, the time complexity is O(N).
• Auxiliary Space : O(1). 
  Any extra space is not required, so the space complexity is constant.