Find the missing number in unordered Arithmetic Progression
Last Updated :
10 Aug, 2022
Given an unsorted array arr[] of N integers that are in Arithmetic Progression, the task is to print the missing element from the given series.
Examples:
Input: arr[] = {12, 3, 6, 15, 18}
Output: 9
Explanation:
The elements given in order are: 3, 6, 12, 15, 18.
Hence missing element is 9.
Input: arr[] = {2, 8, 6, 10}
Output: 4
Explanation:
The elements given in order are: 2, 6, 8, 10.
Hence missing element is 4.
Naive Approach: The idea is to use Binary Search. Sort the given array then the array will arranged in sorted order of AP series, we can apply Binary Search (as in this article) as described below:
- Find the middle element and check if the difference between the middle element and the next element to the middle element is equal to common difference or not, if not then the missing element lies between mid and mid + 1.
- If the middle element is equal to (N/2)th term in the given Arithmetic Series, then the missing element lies in the right side of the middle element.
- Else the element lies in the left side of the middle element.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findMissing(int arr[], int left,
int right, int diff)
{
if (right <= left)
return INT_MAX;
int mid = left + (right - left) / 2;
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0
&& arr[mid] - arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissing(arr, mid + 1,
right, diff);
return findMissing(arr, left,
mid - 1, diff);
}
int missingElement(int arr[], int n)
{
sort(arr, arr + n);
int diff = (arr[n - 1] - arr[0]) / n;
return findMissing(arr, 0, n - 1, diff);
}
int main()
{
int arr[] = { 2, 8, 6, 10 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << missingElement(arr, n);
return 0;
}
|
Java
import java.util.Arrays;
class GFG{
static int findMissing(int arr[], int left,
int right, int diff)
{
if (right <= left)
return 0;
int mid = left + (right - left) / 2;
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 &&
arr[mid] - arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissing(arr, mid + 1,
right, diff);
return findMissing(arr, left,
mid - 1, diff);
}
static int missingElement(int arr[], int n)
{
Arrays.sort(arr);
int diff = (arr[n - 1] - arr[0]) / n;
return findMissing(arr, 0, n - 1, diff);
}
public static void main(String[] args)
{
int arr[] = new int[]{ 2, 8, 6, 10 };
int n = arr.length;
System.out.println(missingElement(arr, n));
}
}
|
Python3
import sys
def findMissing(arr, left, right, diff):
if (right <= left):
return sys.maxsize
mid = left + (right - left) // 2
if (arr[mid + 1] - arr[mid] != diff):
return (arr[mid] + diff)
if (mid > 0 and
arr[mid] - arr[mid - 1] != diff):
return (arr[mid - 1] + diff)
if (arr[mid] == arr[0] + mid * diff):
return findMissing(arr, mid + 1,
right, diff)
return findMissing(arr, left,
mid - 1, diff)
def missingElement(arr, n):
arr.sort()
diff = (arr[n - 1] - arr[0]) // n
return findMissing(arr, 0, n - 1, diff)
arr = [ 2, 8, 6, 10 ]
n = len(arr)
print(missingElement(arr, n))
|
C#
using System;
class GFG{
static int findMissing(int []arr, int left,
int right, int diff)
{
if (right <= left)
return 0;
int mid = left + (right - left) / 2;
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 &&
arr[mid] - arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissing(arr, mid + 1,
right, diff);
return findMissing(arr, left,
mid - 1, diff);
}
static int missingElement(int []arr, int n)
{
Array.Sort(arr);
int diff = (arr[n - 1] - arr[0]) / n;
return findMissing(arr, 0, n - 1, diff);
}
public static void Main(String[] args)
{
int []arr = new int[]{ 2, 8, 6, 10 };
int n = arr.Length;
Console.WriteLine(missingElement(arr, n));
}
}
|
Javascript
<script>
function findMissing(arr, left, right, diff)
{
if (right <= left)
return 0;
let mid = left + parseInt((right - left) / 2, 10);
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 &&
arr[mid] - arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissing(arr, mid + 1,
right, diff);
return findMissing(arr, left,
mid - 1, diff);
}
function missingElement(arr, n)
{
arr.sort(function(a, b){return a - b});
let diff = parseInt((arr[n - 1] -
arr[0]) / n, 10);
return findMissing(arr, 0, n - 1, diff);
}
let arr = [ 2, 8, 6, 10 ];
let n = arr.length;
document.write(missingElement(arr, n));
</script>
|
Time Complexity: O(N*log2N)
Auxiliary Space: O(1) as it is using constant space
Efficient Approach: To optimize the above method we will use the following properties of XOR that is a ^ a = 0, hence, (a ^ b ^ c) ^ (a ^ c) = b. Below are the steps:
- Find the maximum and minimum elements from the given array.
- Find the common difference as:
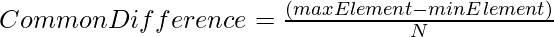
- Calculate xor for all elements in the array.
- Perform xor with all the elements of the actual series to find the resultant value is the missing element.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int missingElement(int arr[], int n)
{
int max_ele = arr[0];
int min_ele = arr[0];
int x = 0;
int d;
for (int i = 0; i < n; i++) {
if (arr[i] > max_ele)
max_ele = arr[i];
if (arr[i] < min_ele)
min_ele = arr[i];
}
d = (max_ele - min_ele) / n;
for (int i = 0; i < n; i++) {
x = x ^ arr[i];
}
for (int i = 0; i <= n; i++) {
x = x ^ (min_ele + (i * d));
}
return x;
}
int main()
{
int arr[] = { 12, 3, 6, 15, 18 };
int n = sizeof(arr) / sizeof(arr[0]);
int element = missingElement(arr, n);
cout << element;
}
|
Java
class GFG{
static int missingElement(int arr[], int n)
{
int max_ele = arr[0];
int min_ele = arr[0];
int x = 0;
int d;
for(int i = 0; i < n; i++)
{
if (arr[i] > max_ele)
max_ele = arr[i];
if (arr[i] < min_ele)
min_ele = arr[i];
}
d = (max_ele - min_ele) / n;
for(int i = 0; i < n; i++)
{
x = x ^ arr[i];
}
for(int i = 0; i <= n; i++)
{
x = x ^ (min_ele + (i * d));
}
return x;
}
public static void main(String[] args)
{
int arr[] = new int[]{ 12, 3, 6, 15, 18 };
int n = arr.length;
int element = missingElement(arr, n);
System.out.print(element);
}
}
|
Python3
def missingElement(arr, n):
max_ele = arr[0]
min_ele = arr[0]
x = 0
d = 0
for i in range(n):
if (arr[i] > max_ele):
max_ele = arr[i]
if (arr[i] < min_ele):
min_ele = arr[i]
d = (max_ele - min_ele) // n
for i in range(n):
x = x ^ arr[i]
for i in range(n + 1):
x = x ^ (min_ele + (i * d))
return x
if __name__ == '__main__':
arr = [ 12, 3, 6, 15, 18 ]
n = len(arr)
element = missingElement(arr, n)
print(element)
|
C#
using System;
class GFG{
static int missingElement(int[] arr, int n)
{
int max_ele = arr[0];
int min_ele = arr[0];
int x = 0;
int d;
for(int i = 0; i < n; i++)
{
if (arr[i] > max_ele)
max_ele = arr[i];
if (arr[i] < min_ele)
min_ele = arr[i];
}
d = (max_ele - min_ele) / n;
for(int i = 0; i < n; i++)
{
x = x ^ arr[i];
}
for(int i = 0; i <= n; i++)
{
x = x ^ (min_ele + (i * d));
}
return x;
}
public static void Main()
{
int[] arr = new int[]{ 12, 3, 6, 15, 18 };
int n = arr.Length;
int element = missingElement(arr, n);
Console.Write(element);
}
}
|
Javascript
<script>
function missingElement(arr, n)
{
let max_ele = arr[0];
let min_ele = arr[0];
let x = 0;
let d;
for (let i = 0; i < n; i++) {
if (arr[i] > max_ele)
max_ele = arr[i];
if (arr[i] < min_ele)
min_ele = arr[i];
}
d = parseInt((max_ele - min_ele) / n, 10);
for (let i = 0; i < n; i++) {
x = x ^ arr[i];
}
for (let i = 0; i <= n; i++) {
x = x ^ (min_ele + (i * d));
}
return x;
}
let arr = [ 12, 3, 6, 15, 18 ];
let n = arr.length;
let element = missingElement(arr, n);
document.write(element);
</script>
|
Time complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...