Find the minimum value of the given expression over all pairs of the array
Last Updated :
18 Nov, 2021
Given an array A of size N, find the minimum value of the expression : 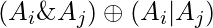 over all pairs (i, j) (where i != j). Here
over all pairs (i, j) (where i != j). Here 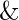 ,
,  and
and  represent bitwise AND, bitwise OR and bitwise XOR resprectively.
represent bitwise AND, bitwise OR and bitwise XOR resprectively.
Examples:
Input: A = [1, 2, 3, 4, 5]
Output: 1
Explanation:
(A[1] and A[2]) xor (A[1] or A[2]) = 1,
which is minimum possible value.
Input : A = [12, 3, 14, 5, 9, 8]
Output : 1
Naive Approach:
Iterate through all the pairs of the array with different index and find the minimum possible value of given expression over them.
Below the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int MinimumValue(int a[], int n)
{
int answer = INT_MAX;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
answer = min(answer,
((a[i] & a[j])
^ (a[i] | a[j])));
}
}
return answer;
}
int main()
{
int N = 6;
int A[N] = { 12, 3, 14, 5, 9, 8 };
cout << MinimumValue(A, N);
return 0;
}
|
Java
import java.io.*;
import java.util.Arrays;
class GFG
{
static int MinimumValue(int a[], int n)
{
int answer = Integer.MAX_VALUE;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
answer = Math.min(answer, ((a[i] & a[j])
^ (a[i] | a[j])));
}
}
return answer;
}
public static void main(String[] args)
{
int N = 6;
int[] A = new int[]{ 12, 3, 14, 5, 9, 8 };
System.out.print(MinimumValue(A, N));
}
}
|
Python3
import sys
def MinimumValue(a,n):
answer = sys.maxsize
for i in range(n):
for j in range(i + 1, n, 1):
answer = min(answer,((a[i] & a[j])^(a[i] | a[j])))
return answer
if __name__ == '__main__':
N = 6
A = [12, 3, 14, 5, 9, 8]
print(MinimumValue(A, N))
|
C#
using System;
class GFG{
static int MinimumValue(int []a, int n)
{
int answer = Int32.MaxValue;
for(int i = 0; i < n; i++)
{
for(int j = i + 1; j < n; j++)
{
answer = Math.Min(answer,
((a[i] & a[j]) ^
(a[i] | a[j])));
}
}
return answer;
}
public static void Main()
{
int N = 6;
int[] A = new int[]{ 12, 3, 14, 5, 9, 8 };
Console.Write(MinimumValue(A, N));
}
}
|
Javascript
<script>
function MinimumValue(a, n)
{
let answer = Number.MAX_SAFE_INTEGER;
for (let i = 0; i < n; i++)
{
for (let j = i + 1; j < n; j++)
{
answer = Math.min(answer,
((a[i] & a[j])
^ (a[i] | a[j])));
}
}
return answer;
}
let N = 6;
let A = [ 12, 3, 14, 5, 9, 8 ];
document.write(MinimumValue(A, N));
</script>
|
Time Complexity : O(N2)
Auxiliary Space: O(1)
Efficient Approach
- Let’s simplify the given expression :
+ represents bitwise OR
. represents bitwise AND
^ represents bitwise XOR
‘ represents 1’s complement
(x . y) ^ (x + y) = (x . y) . (x + y)’ + (x . y)’ . (x + y) (using definition of XOR)
= (x . y) . (x’ . y’) + (x’+ y’) . (x + y) (De morgan’s law)
= x.x’.y.y’ + x’.x + x’.y + y’.x + y.y
= 0 + 0 + x’.y + y’.x + 0
= x ^ y
- Since the expression simplifies to minimum xor value pair, we can simply use the algorithm mentioned in this article to find the same efficiently.
Below the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int MinimumValue(int arr[], int n)
{
sort(arr, arr + n);
int minXor = INT_MAX;
int val = 0;
for (int i = 0; i < n - 1; i++)
{
val = arr[i] ^ arr[i + 1];
minXor = min(minXor, val);
}
return minXor;
}
int main()
{
int N = 6;
int A[N] = { 12, 3, 14, 5, 9, 8 };
cout << MinimumValue(A, N);
return 0;
}
|
Java
import java.io.*;
import java.util.Arrays;
class GFG {
static int MinimumValue(int arr[], int n)
{
Arrays.sort(arr);
int minXor = Integer.MAX_VALUE;
int val = 0;
for(int i = 0; i < n - 1; i++)
{
val = arr[i] ^ arr[i + 1];
minXor = Math.min(minXor, val);
}
return minXor;
}
public static void main(String[] args)
{
int N = 6;
int[] A = new int[]{ 12, 3, 14, 5, 9, 8 };
System.out.print(MinimumValue(A, N));
}
}
|
Python3
import sys
def MinimumValue(arr, n):
arr.sort();
minXor = sys.maxsize;
val = 0;
for i in range(0, n - 1):
val = arr[i] ^ arr[i + 1];
minXor = min(minXor, val);
return minXor;
if __name__ == '__main__':
N = 6;
A = [ 12, 3, 14, 5, 9, 8 ];
print(MinimumValue(A, N));
|
C#
using System;
class GFG{
static int MinimumValue(int []arr, int n)
{
Array.Sort(arr);
int minXor = Int32.MaxValue;
int val = 0;
for(int i = 0; i < n - 1; i++)
{
val = arr[i] ^ arr[i + 1];
minXor = Math.Min(minXor, val);
}
return minXor;
}
public static void Main()
{
int N = 6;
int[] A = new int[]{ 12, 3, 14, 5, 9, 8 };
Console.Write(MinimumValue(A, N));
}
}
|
Javascript
<script>
function MinimumValue(arr, n)
{
arr.sort();
let minXor = Number.MAX_VALUE;
let val = 0;
for (let i = 0; i < n - 1; i++)
{
val = arr[i] ^ arr[i + 1];
minXor = Math.min(minXor, val);
}
return minXor;
}
let N = 6;
let A = [ 12, 3, 14, 5, 9, 8 ];
document.write(MinimumValue(A, N));
</script>
|
Time Complexity : O(N * log(N))
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...