Find the longest common prefix between two strings after performing swaps on second string

Last Updated : 21 May, 2021

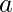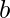Given two strings $a$ and $b$ . Find the longest common prefix between them after performing zero or more operations on string 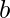$b$ . In each operation, you can swap any two letters.
Examples:

Input : a = "here", b = "there"
Output : 4
The 2nd string can be made "heret" by just 
swapping characters and thus the longest
prefix is of length 4.

Input : a = "you", b = "me"
Output : 0

Given that we are only allowed to performs swaps in the string 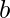$b$ and the length of prefix should be maximized. So the idea is to traverse string 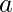$a$ and check if the frequency of current character in string 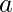$a$ is same or less of that in string 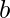$b$ . If yes then move forward in string an otherwise break and print the length of the part of string an up to which a character is matched in string $b$ .
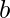Below is the implementation of the above approach:

C++

// C++ program to find the longest
// common prefix between two strings
// after performing swaps on the second string
#include <bits/stdc++.h>
using namespace std;
 
  
void LengthLCP(string x, string y)
{
     
 
    int fr[26]={0};
      
    int a = x.length(); // length of x
    int b = y.length(); // length of y
      
    for (int i=0 ;i<b ; i++)
    {
        // creating frequency array of
        // characters of y
        fr[y[i] - 97] += 1;
    }
    // storing the length of
    // longest common prefix
    int c = 0;
      
    for (int i=0 ;i<a ; i++)
    {
        // checking if the frequency of the character at
        // position i in x in b is greater than zero or not
        // if zero we increase the prefix count by 1
        if (fr[x[i] - 97] > 0){
            c += 1;
            fr[x[i] - 97] -= 1;
        }
        else
            break;
    }
    cout<<(c)<<endl;
}
// Driver Code
int main()
{
string x="here", y =  "there";
  
LengthLCP(x, y);
 
return 0;
}
//contributed by Arnab Kundu

Java

// Java program to find the longest
// common prefix between two strings
// after performing swaps on the second string
 
public class GFG {
 
    static void LengthLCP(String x, String y)
    {
         
 
        int fr[]=new int [26];
          
        int a = x.length(); // length of x
        int b = y.length(); // length of y
          
        for (int i=0 ;i<b ; i++)
        {
            // creating frequency array of
            // characters of y
            fr[y.charAt(i) - 97] += 1;
        }
        // storing the length of
        // longest common prefix
        int c = 0;
          
        for (int i=0 ;i<a ; i++)
        {
            // checking if the frequency of the character at
            // position i in x in b is greater than zero or not
            // if zero we increase the prefix count by 1
            if (fr[x.charAt(i) - 97] > 0){
                c += 1;
                fr[x.charAt(i) - 97] -= 1;
            }
            else
                break;
        }
        System.out.println((c)) ;
    }
 
 
    public static void main(String args[])
    {
        String x="here", y =  "there";
          
        LengthLCP(x, y);
 
 
    }
    // This code is contributed by ANKITRAI1
}
  

Python3

# Python program to find the longest
# common prefix between two strings
# after performing swaps on the second string
 
def LengthLCP(x, y):
    fr = [0] * 26
     
    a = len(x) # length of x
    b = len(y) # length of y
     
    for i in range(b):
        # creating frequency array of
        # characters of y
        fr[ord(y[i]) - 97] += 1
     
    # storing the length of
    # longest common prefix
    c = 0
     
    for i in range(a):
        # checking if the frequency of the character at
        # position i in x in b is greater than zero or not
        # if zero we increase the prefix count by 1
        if (fr[ord(x[i]) - 97] > 0):
            c += 1
            fr[ord(x[i]) - 97] -= 1
        else:
            break
    print(c)
 
# Driver Code
 
x, y = "here", "there"
 
LengthLCP(x, y)

C#

// C# program to find the longest
// common prefix between two strings
// after performing swaps on the
// second string
using System;
 
class GFG
{
 
static void LengthLCP(String x, String y)
{
    int []fr = new int [26];
     
    int a = x.Length; // length of x
    int b = y.Length; // length of y
     
    for (int i = 0 ; i < b; i++)
    {
        // creating frequency array
        // of characters of y
        fr[y[i] - 97] += 1;
    }
     
    // storing the length of
    // longest common prefix
    int c = 0;
     
    for (int i = 0 ; i < a; i++)
    {
        // checking if the frequency of
        // the character at position i
        // in x in b is greater than zero
        // or not if zero we increase the
        // prefix count by 1
        if (fr[x[i] - 97] > 0)
        {
            c += 1;
            fr[x[i] - 97] -= 1;
        }
        else
            break;
    }
    Console.Write((c)) ;
}
 
// Driver Code
public static void Main()
{
    String x = "here", y = "there";
     
    LengthLCP(x, y);
}
}
 
// This code is contributed by 29AjayKumar

PHP

<?php
// PHP program to find the longest
// common prefix between two strings
// after performing swaps on the second string
 
function LengthLCP($x, $y)
{
     
 
    $fr = array_fill(0,26,NULL);
     
    $a = strlen($x); // length of x
    $b = strlen($y); // length of y
     
    for ($i = 0 ;$i < $b ; $i++)
    {
        // creating frequency array of
        // characters of y
        $fr[ord($y[$i]) - 97] += 1;
    }
     
    // storing the length of
    // longest common prefix
    $c = 0;
     
    for ($i = 0 ;$i < $a ; $i++)
    {
        // checking if the frequency of the character at
        // position i in x in b is greater than zero or not
        // if zero we increase the prefix count by 1
        if ($fr[ord($x[$i]) - 97] > 0)
        {
            $c += 1;
            $fr[ord($x[$i]) - 97] -= 1;
        }
        else
            break;
    }
    echo $c;
}
 
// Driver Code
$x="here";
$y = "there";
 
LengthLCP($x, $y);
 
return 0;
 
// This code is contributed by ChitraNayal
?>

Javascript

<script>
 
// JavaScript program to find the long
// common prefix between two strings
// after performing swaps on the second string
 
    function LengthLCP(x, y)
    {
           
   
        let fr = Array(26).fill(0);
            
        let a = x.length; // length of x
        let b = y.length; // length of y
            
        for (let i=0 ;i<b ; i++)
        {
            // creating frequency array of
            // characters of y
            fr[y[i].charCodeAt() - 97] += 1;
        }
        // storing the length of
        // longest common prefix
        let c = 0;
            
        for (let i=0 ;i<a ; i++)
        {
            // checking if the
            // frequency of the character at
            // position i in x in b is greater
            // than zero or not
            // if zero we increase the
            // prefix count by 1
            if (fr[x[i].charCodeAt() - 97] > 0){
                c += 1;
                fr[x[i].charCodeAt() - 97] -= 1;
            }
            else
                break;
        }
        document.write((c)) ;
    }
 
 
// driver code
 
    let x="here", y =  "there";
            
        LengthLCP(x, y);
   
</script>

Output:

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

My Personal Notes