Find the ln(X) and log10X with the help of expansion
Last Updated :
09 Feb, 2023
Given a positive number x, the task is to find the natural log (ln) and log to the base 10 (log10) of this number with the help of expansion.
Example:
Input: x = 5
Output: ln 5.000 = 1.609
log10 5.000 = 0.699
Input: x = 10
Output: ln 10.000 = 2.303
log10 10.000 = 1.000
Approach:
- The expansion of natural logarithm of x (ln x) is:
&space;=&space;2[(\frac{x-1}{x+1})+\frac{(\frac{x-1}{x+1})^{3}}{3}+\frac{(\frac{x-1}{x+1})^{5}}{5}+...+\frac{(\frac{x-1}{x+1})^{2n-1}}{2n-1}]&space;})
- Therefore this series can be summed up as:
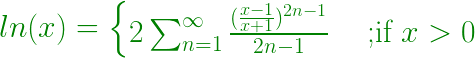
- Hence a function can be made to evaluate the nth term of the sequence for 1 ? x ? n
- Now to calculate log10 x, below formula can be used:

Below is the implementation of the above approach:
C++
#include <cmath>
#include <iomanip>
#include <iostream>
using namespace std;
double calculateLnx(double n)
{
double num, mul, cal, sum = 0;
num = (n - 1) / (n + 1);
for (int i = 1; i <= 1000; i++) {
mul = (2 * i) - 1;
cal = pow(num, mul);
cal = cal / mul;
sum = sum + cal;
}
sum = 2 * sum;
return sum;
}
double calculateLogx(double lnx)
{
return (lnx / 2.303);
}
int main()
{
double lnx, logx, n = 5;
lnx = calculateLnx(n);
logx = calculateLogx(lnx);
cout << fixed << setprecision(3)
<< "ln " << n << " = "
<< lnx << endl;
cout << fixed << setprecision(3)
<< "log10 " << n << " = "
<< logx << endl;
}
|
Java
import java.io.*;
class GFG
{
static double calculateLnx(double n)
{
double num, mul, cal, sum = 0;
num = (n - 1) / (n + 1);
for (int i = 1; i <= 1000; i++)
{
mul = (2 * i) - 1;
cal = Math.pow(num, mul);
cal = cal / mul;
sum = sum + cal;
}
sum = 2 * sum;
return sum;
}
static double calculateLogx(double lnx)
{
return (lnx / 2.303);
}
public static void main (String[] args)
{
double lnx, logx, n = 5;
lnx = calculateLnx(n);
logx = calculateLogx(lnx);
System.out.println ("ln " + n + " = " + lnx );
System.out.println ("log10 " + n + " = "+ logx );
}
}
|
Python3
from math import pow
def calculateLnx(n):
sum = 0
num = (n - 1) / (n + 1)
for i in range(1, 1001, 1):
mul = (2 * i) - 1
cal = pow(num, mul)
cal = cal / mul
sum = sum + cal
sum = 2 * sum
return sum
def calculateLogx(lnx):
return (lnx / 2.303)
if __name__ == '__main__':
n = 5
lnx = calculateLnx(n)
logx = calculateLogx(lnx)
print("ln", "{0:.3f}".format(n),
"=", "{0:.3f}".format(lnx))
print("log10", "{0:.3f}".format(n),
"=", "{0:.3f}".format(logx))
|
C#
using System;
class GFG
{
static double calculateLnx(double n)
{
double num, mul, cal, sum = 0;
num = (n - 1) / (n + 1);
for (int i = 1; i <= 1000; i++)
{
mul = (2 * i) - 1;
cal = Math.Pow(num, mul);
cal = cal / mul;
sum = sum + cal;
}
sum = 2 * sum;
return sum;
}
static double calculateLogx(double lnx)
{
return (lnx / 2.303);
}
public static void Main (String[] args)
{
double lnx, logx, n = 5;
lnx = calculateLnx(n);
logx = calculateLogx(lnx);
Console.WriteLine("ln " + n + " = " + lnx );
Console.WriteLine("log10 " + n + " = "+ logx );
}
}
|
Javascript
<script>
function calculateLnx(n)
{
let num, mul, cal, sum = 0;
num = (n - 1) / (n + 1);
for(let i = 1; i <= 1000; i++)
{
mul = (2 * i) - 1;
cal = Math.pow(num, mul);
cal = cal / mul;
sum = sum + cal;
}
sum = 2 * sum;
return sum;
}
function calculateLogx(lnx)
{
return (lnx / 2.303);
}
let lnx, logx, n = 5;
lnx = calculateLnx(n);
logx = calculateLogx(lnx);
document.write("ln " + n + " = " + lnx + "<br>");
document.write("log10 " + n + " = "+ logx + "<br>");
</script>
|
Output
ln 5.000 = 1.609
log10 5.000 = 0.699
Time complexity: O(1000), as the loop iterates 1000 times.
Auxiliary Space: O(1),
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...