Find the length of Kth N-sided polygon formed by given operations

Given an integer L, representing the side length of an N-sided regular polygon and integer K, the task is to find the side length of the K^th N-sided regular polygon formed inside the (K – 1)^th regular polygon by connecting midpoints of the sides of the (K – 1)^th polygon.

Examples:

Input: N = 3, L = 6, K = 2
Output: 3

Input: N = 5, L = 21, K = 7
Output: 5.88796

Approach: The given problem can be solved based on the following observations:

• Suppose,  \theta represents the interior angle of the N-sided polygon which is the same for all the polygons formed inside i.e., 
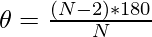
• The length of the side of the first polygon formed inside by connecting midpoints of the sides can be calculated using the formula as .
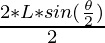• The length of the side of the K^th polygon formed inside the (K – 1)^th polygon and connecting midpoints of the sides of the (K – 1)^th polygon is 

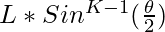
Follow the steps below to solve the problem:

• Find the interior angle of the N-sided regular polygon and store it in a variable say angle in radians.
• Print the side length after calculating the side length of K^th N sided regular polygon by the above-discussed formula .

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;
#define PI 3.14159265

// Function to calculate the interior
// angle of a N-sided regular polygon
double findInteriorAngle(int n)
{
    return (n - 2) * PI / n;
}

// Function to find the K-th polygon
// formed inside the (K - 1)th polygon
double calculateSideLength(double L,
                           int N, int K)
{
    // Stores the interior angle
    double angle = findInteriorAngle(N);

    // Stores the side length of
    // K-th regular polygon
    double length = L * pow(sin(angle / 2),
                            (K - 1));

    // Return the length
    return length;
}

// Driver Code
int main()
{
    double N = 5, L = 21, K = 7;
    cout << calculateSideLength(L, N, K);

    return 0;
}

Java

// Java program for the above approach
import java.util.*;

class GFG{

static final double PI = 3.14159265;

// Function to calculate the interior
// angle of a N-sided regular polygon
static double findInteriorAngle(int n)
{
    return ((n - 2) * PI) / n;
}

// Function to find the K-th polygon
// formed inside the (K - 1)th polygon
static double calculateSideLength(double L,
                                  int N, int K)
{

    // Stores the interior angle
    double angle = findInteriorAngle(N);

    // Stores the side length of
    // K-th regular polygon
    double length = L * Math.pow(Math.sin(angle / 2),
                                             (K - 1));

    // Return the length
    return length;
}

// Driver Code
public static void main(String[] args)
{
    double L = 21;
    int N = 5, K = 7;

    System.out.print(calculateSideLength(L, N, K));
}
}

// This code is contributed by 29AjayKumar

Python3

# Python3 program for the above approach
import math
PI = 3.14159265

# Function to calculate the interior
# angle of a N-sided regular polygon
def findInteriorAngle(n):

    return (n - 2) * PI / n

# Function to find the K-th polygon
# formed inside the (K - 1)th polygon
def calculateSideLength(L,
                        N, K):

    # Stores the interior angle
    angle = findInteriorAngle(N)

    # Stores the side length of
    # K-th regular polygon
    length = L * pow(math.sin(angle / 2),
                     (K - 1))

    # Return the length
    return length


# Driver Code
if __name__ == "__main__":

    N = 5
    L = 21
    K = 7
    print(calculateSideLength(L, N, K))

    # This code is contributed by ukasp.

C#

// C# program for the above approach
using System;

class GFG{

static readonly double PI = 3.14159265;

// Function to calculate the interior
// angle of a N-sided regular polygon
static double findInteriorAngle(int n)
{
    return ((n - 2) * PI) / n;
}

// Function to find the K-th polygon
// formed inside the (K - 1)th polygon
static double calculateSideLength(double L,
                                  int N, int K)
{

    // Stores the interior angle
    double angle = findInteriorAngle(N);

    // Stores the side length of
    // K-th regular polygon
    double length = L * Math.Pow(Math.Sin(angle / 2),
                                             (K - 1));

    // Return the length
    return length;
}

// Driver Code
public static void Main(String[] args)
{
    double L = 21;
    int N = 5, K = 7;

    Console.Write(calculateSideLength(L, N, K));
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

        // Javascript program for the above approach
        const PI = 3.14159265

        // Function to calculate the interior
        // angle of a N-sided regular polygon
        function findInteriorAngle(n)
        {
            return (n - 2) * PI / n;
        }

        // Function to find the K-th polygon
        // formed inside the (K - 1)th polygon
        function calculateSideLength(L,
            N, K) {
            // Stores the interior angle
            let angle = findInteriorAngle(N);

            // Stores the side length of
            // K-th regular polygon
            let length = L * Math.pow(Math.sin(angle / 2),
                (K - 1));

            // Return the length
            return length;
        }

        // Driver Code

        let N = 5
        let L = 21
        let K = 7;
        document.write(calculateSideLength(L, N, K))

    </script>

Output:

5.88796

Time Complexity: O(log K)
Auxiliary Space: O(1),  since no extra space has been taken.