Find the Largest N digit perfect square number in Base B
Last Updated :
03 Apr, 2023
Given two integers N and B, the task is to find the largest N digit numbers of Base B which is a perfect square.
Examples:
Input: N = 2, B = 10
Output: 81
Explanation:
81 is the largest 2-digit perfect square in base 10.
Input: N = 1, B = 8
Output: 4
Explanation:
4 is the largest 1 digit Octal number which is also a perfect square.
Brute Force Approach:
1) isPerfectSquare checks if a given number is a perfect square.
2) decimalToBase converts a decimal number to any base.
3) largestNDigitPerfectSquare finds the largest N digit perfect square in base B.
largestNDigitPerfectSquare function first calculates the largest N digit number in base B. It then iterates over all numbers starting from this largest number and checks whether each number is a perfect square in decimal. If a perfect square is found, it converts it to base B and returns it.
Implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPerfectSquare(int n) {
int root = sqrt(n);
return (root * root == n);
}
int decimalToBase(int n, int base) {
int num = 0, count = 0;
while (n != 0) {
int rem = n % base;
num += rem * pow(10, count);
count++;
n /= base;
}
return num;
}
int largestNDigitPerfectSquare(int N, int B) {
int largestNum = pow(B, N) - 1;
for (int i = largestNum; i >= 0; i--) {
int decimalNum = 0, count = 0;
int num = i;
while (num != 0) {
int rem = num % 10;
decimalNum += rem * pow(B, count);
count++;
num /= 10;
}
if (isPerfectSquare(decimalNum)) {
return decimalToBase(decimalNum, B);
}
}
return -1;
}
int main() {
int N = 2, B = 10;
int largestPerfectSquare = largestNDigitPerfectSquare(N, B);
cout << largestPerfectSquare << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
static boolean isPerfectSquare(int n) {
int root = (int)Math.sqrt(n);
return (root * root == n);
}
static int decimalToBase(int n, int base) {
int num = 0, count = 0;
while (n != 0) {
int rem = n % base;
num += rem * (int)Math.pow(10, count);
count++;
n /= base;
}
return num;
}
static int largestNDigitPerfectSquare(int N, int B) {
int largestNum = (int)Math.pow(B, N) - 1;
for (int i = largestNum; i >= 0; i--) {
int decimalNum = 0, count = 0;
int num = i;
while (num != 0) {
int rem = num % 10;
decimalNum += rem * (int)Math.pow(B, count);
count++;
num /= 10;
}
if (isPerfectSquare(decimalNum)) {
return decimalToBase(decimalNum, B);
}
}
return -1;
}
public static void main(String[] args) {
int N = 2, B = 10;
int largestPerfectSquare = largestNDigitPerfectSquare(N, B);
System.out.println(largestPerfectSquare);
}
}
|
Python3
import math
def is_perfect_square(n):
root = int(math.sqrt(n))
return root * root == n
def decimal_to_base(n, base):
num, count = 0, 0
while n != 0:
rem = n % base
num += rem * (10 ** count)
count += 1
n //= base
return num
def largest_n_digit_perfect_square(N, B):
largest_num = B ** N - 1
for i in range(largest_num, -1, -1):
decimal_num, count = 0, 0
num = i
while num != 0:
rem = num % 10
decimal_num += rem * (B ** count)
count += 1
num //= 10
if is_perfect_square(decimal_num):
return decimal_to_base(decimal_num, B)
return -1
if __name__ == '__main__':
N, B = 2, 10
largest_perfect_square = largest_n_digit_perfect_square(N, B)
print(largest_perfect_square)
|
Javascript
function isPerfectSquare(n) {
let root = Math.floor(Math.sqrt(n));
return root * root === n;
}
function decimalToBase(n, base) {
let num = 0, count = 0;
while (n !== 0) {
let rem = n % base;
num += rem * Math.pow(10, count);
count++;
n = Math.floor(n / base);
}
return num;
}
function largestNDigitPerfectSquare(N, B) {
let largestNum = Math.pow(B, N) - 1;
for (let i = largestNum; i >= 0; i--) {
let decimalNum = 0, count = 0, num = i;
while (num !== 0) {
let rem = num % 10;
decimalNum += rem * Math.pow(B, count);
count++;
num = Math.floor(num / 10);
}
if (isPerfectSquare(decimalNum)) {
return decimalToBase(decimalNum, B);
}
}
return -1;
}
let N = 2, B = 10;
let largestPerfectSquare = largestNDigitPerfectSquare(N, B);
console.log(largestPerfectSquare);
|
C#
using System;
class Program {
static bool isPerfectSquare(int n) {
int root = (int) Math.Sqrt(n);
return (root * root == n);
}
static int decimalToBase(int n, int b) {
int num = 0, count = 0;
while (n != 0) {
int rem = n % b;
num += rem * (int) Math.Pow(10, count);
count++;
n /= b;
}
return num;
}
static int largestNDigitPerfectSquare(int N, int B) {
int largestNum = (int) Math.Pow(B, N) - 1;
for (int i = largestNum; i >= 0; i--) {
int decimalNum = 0, count = 0;
int num = i;
while (num != 0) {
int rem = num % 10;
decimalNum += rem * (int) Math.Pow(B, count);
count++;
num /= 10;
}
if (isPerfectSquare(decimalNum)) {
return decimalToBase(decimalNum, B);
}
}
return -1;
}
static void Main(string[] args) {
int N = 2, B = 10;
int largestPerfectSquare = largestNDigitPerfectSquare(N, B);
Console.WriteLine(largestPerfectSquare);
}
}
|
Time Complexity: O(B^N), where B and N are given in the problem statement
Space Complexity: O(1)
Approach: The largest number N in base B is given by 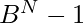 . So if we find the square root of this number in integer form and then we have to again do its square then it will be the largest perfect square of N digits which is given by the formula:
. So if we find the square root of this number in integer form and then we have to again do its square then it will be the largest perfect square of N digits which is given by the formula: 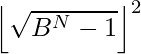 .
.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void nDigitPerfectSquares(int n, int b)
{
int largest
= pow(ceil(sqrt(pow(b, n))) - 1, 2);
cout << largest;
}
int main()
{
int N = 1, B = 8;
nDigitPerfectSquares(N, B);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static double nDigitPerfectSquares(int n, int b)
{
double largest = Math.pow(Math.ceil
(Math.sqrt
(Math.pow(b, n))) - 1, 2);
return largest;
}
public static void main(String[] args)
{
int N = 1, B = 8;
System.out.println(nDigitPerfectSquares(N, B));
}
}
|
Python3
import math
def nDigitPerfectSquares(n, b):
largest = pow(math.ceil
(math.sqrt(pow(b, n))) - 1, 2)
print(largest)
N = 1
B = 8
nDigitPerfectSquares(N, B)
|
Javascript
<script>
function nDigitPerfectSquares(n, b)
{
var largest
= Math.pow(Math.ceil(Math.sqrt(Math.pow(b, n))) - 1, 2);
document.write(largest);
}
var N = 1, B = 8;
nDigitPerfectSquares(N, B);
</script>
|
C#
using System;
class GFG {
static double nDigitPerfectSquares(int n, int b)
{
double largest = Math.Pow(Math.Ceiling
(Math.Sqrt
(Math.Pow(b, n))) - 1, 2);
return largest;
}
public static void Main(String[] args)
{
int N = 1, B = 8;
Console.WriteLine(nDigitPerfectSquares(N, B));
}
}
|
Time Complexity: O(logn)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...