Find the element at R’th row and C’th column in given a 2D pattern
Last Updated :
07 Feb, 2023
Given two integers R and C, the task is to find the element at the Rth row and Cth column.
Pattern:
- First Element of ith row =
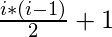
- Every element is a Arithmetic progression increasing difference where common difference is 1.
- Initial Difference Term =
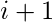
Examples:
Input: R = 4, C = 4
Output: 25
Explanation:
Pattern of size 4 * 4 is –
1 3 6 10
2 5 9 14
4 8 13 19
7 12 18 25
Therefore, Element at Pat[4][4] = 25
Input: R = 3, C = 3
Output: 13
Explanation:
Pattern of size 3 * 3 is –
1 3 6
2 5 9
4 8 13
Therefore, element at Pat[3][3] = 13
Naive Approach: A simple solution is to generate the pattern matrix of size R * C and then finally return the element at the Rth row and Cth column.
Time Complexity: O(R*C)
Auxiliary Space: O(R*C)
Efficient Approach: The idea is to find the first term of the Rth row using the formulae 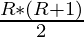 and then finally compute the Cth term of that column using the help of loop.
and then finally compute the Cth term of that column using the help of loop.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int findValue(int R, int C)
{
int k = (R * (R - 1)) / 2 + 1;
int diff = R + 1;
for (int i = 1; i < C; i++) {
k = (k + diff);
diff++;
}
return k;
}
int main()
{
int R = 4;
int C = 4;
int k = findValue(R, C);
cout << k;
return 0;
}
|
Java
import java.io.*;
class GFG{
static int findValue(int R, int C)
{
int k = (R * (R - 1)) / 2 + 1;
int diff = R + 1;
for(int i = 1; i < C; i++)
{
k = (k + diff);
diff++;
}
return k;
}
public static void main (String[] args)
{
int R = 4;
int C = 4;
int k = findValue(R, C);
System.out.println(k);
}
}
|
Python3
def findValue(R, C):
k = (R*(R-1))//2 + 1
diff = R + 1
for i in range(1, C):
k = (k + diff)
diff+= 1
return k
if __name__ == "__main__":
R = 4
C = 4
k = findValue(R, C)
print(k)
|
C#
using System;
class GFG{
static int findValue(int R, int C)
{
int k = (R * (R - 1)) / 2 + 1;
int diff = R + 1;
for(int i = 1; i < C; i++)
{
k = (k + diff);
diff++;
}
return k;
}
public static void Main()
{
int R = 4;
int C = 4;
int k = findValue(R, C);
Console.Write(k);
}
}
|
Javascript
<script>
function findValue(R, C)
{
let k = (R * (R - 1)) / 2 + 1;
let diff = R + 1;
for(let i = 1; i < C; i++)
{
k = (k + diff);
diff++;
}
return k;
}
let R = 4;
let C = 4;
let k = findValue(R, C);
document.write(k);
</script>
|
Time complexity : O(C), where C is the column number. The code iterates C times to find the value in the specified column.
Space complexity : O(1), as it only uses a few variables and arrays of constant size, which means the space required does not increase with increasing input size.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...