In mathematics, arithmetic is concerned with the study of numbers, while keeping the emphasis on the traditional operations relevant to them. These operators are addition, subtraction, multiplication, division, exponents, and radicals. Arithmetic can safely be stated as the foundation for all other branches of mathematics. Geometry, mensuration, trigonometry, etc. all these fields employ the basic arithmetic operations for various mathematical observations, calculations, and conclusions.
Series
Summing up all the terms of a given sequence forms a series of the sequence concerned. Thus, a series is basically a sequence, only with an addition operator between all its terms. Now since a series has been made from a sequence itself, it is only natural that its pattern would exactly be the same as its parent sequence. A series would be definite or indefinite depending upon the concerned sequence itself too.
Examples
- 1 + 2 + 3 + 4 + …. is an infinite series of all the natural numbers.
- 10 + 20 + 30 + 40 is a finite series of the first four multiples of 10.
Infinite Geometric Series
Such a series where every succeeding term is in a constant ratio to its preceding term is called a geometric series. From the definition of a series, it is clear that all the terms constituting a series are in sum with each- other. An infinite series is one that has no end. It implies that in an infinite geometric series, the terms are in a constant ratio to each other and have no end. It is to be noted that the ratio is continuous, i.e., constant throughout the series and is called the common ratio. Another important aspect to be kept in mind is that the absolute value of the common ratio must be greater than zero, i.e, |r| < 0.
In general, a finite geometric series with its first term a, and common ratio r is expressed as,
a, ar, ar2, ar3, ar4, …arn – 2, arn – 1, arn.
However, an infinite geometric series would be depicted as follows,
a, ar, ar2, ar3, ar4, …ar100000,…
For example, the series 2 + 4 + 8 + 16 + 32 + …. is an infinite geometric series because each successive term is obtained by multiplying the previous term by 2, and since the series has no end, i.e., is not finite.
Find the common ratio of an infinite Geometric Series.
Answer:
In simple language, the common ratio of a geometric series means the quantity which is multiplied by each preceding term in order to form the succeeding term. This means that every term after the first one is to be multiplied with a fixed quantity in order to form an infinite geometric series. It also implies that if one were to divide each succeeding term with the term immediately preceding it, the quotient so obtained would be the common ratio of the given series. This is because of the general rule of division in mathematics. Divisor multiplied by quotient yields the dividend. Here, the words divisor, quotient, and dividend pertain to the preceding term, common ratio, and successive terms respectively. The common ratio, r of a geometric series is calculated using the following formula,
r = 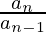
Where n represents the succeeding term and n – 1 is the term immediately preceding the term chosen.
It is to be noted that in order to calculate the common ratio, any random term can be picked up from the given series and divided by its immediately preceding term, and the quotient would be constant throughout the whole series, hence the name ‘common ratio’.
Examples
- The common ratio of the series 3, 9, 27, 81, 243, 729, ….. is = 9/3 = 27/9 = 81/27 = 243/81 = 729/243 = 3.
- The common ratio of the geometric series 10, 100, 1000, 10000, … would be = 100/10 = 1000/100 = 10.
- The common ratio of the series 56, 28, 14, 7,… would be = 56/2 = 28/14 = 14/7 = 2.
Similar Problems
Question 1: Find the common ratio of the series: 27, 9, 3, 1, 1/3, 1/9, 1/27, … and list the next three terms.
Solution:
Common ratio = 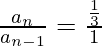 = 1/3.
= 1/3.
The next three terms would be,
1/27 × 1/3 = 1/81
1/81 × 1/3 = 1/243
1/243 × 1/3 = 1/729
Hence the common ratio is 1/3 and the next three terms are 1/81, 1/243, 1/729.
Question 2: Find the common ratio of the series: 5, 25, 125, 625, … and list the next two terms.
Solution:
Common ratio = 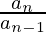 = 25/5 = 5
= 25/5 = 5
The next three terms would be,
625 × 5 = 3125
3125 × 5 = 15625
Hence the common ratio is 5 and the next two terms are 3125 and 15625.
Question 3. Find the common ratio of the series: 25, 5, 1, 1/5, 1/25, … and list the next 4 terms.
Solution:
Common ratio = 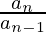 = 5/25 = 1/5
= 5/25 = 1/5
The next 4 terms would be,
1/25 × 1/5 = 1/125
1/125 × 1/5 = 1/625
1/625 × 1/5 = 1/3125
1/3125 × 1/5 = 1/15625
Hence the common ratio is 1/5 and the next 4 terms are 1/125, 1/625, 1/3125 and 1/15625.
Question 4: Find the common ratio of the series: 1/216, 1/36, 1/6, 1, 6, 36, … and list the next 2 terms.
Solution:
Common ratio = 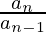 =
= 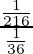 = 6
= 6
The next 2 terms would be,
36 × 6 = 216
216 × 6 = 1296
Hence the common ratio is 6 and the next 2 terms are 216 and 1296.
Question 5: Find the common ratio of the series: 1, 3, 9, 27, 81, … and list the next 4 terms.
Solution:
Common ratio = 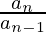 = 3/1 = 3
= 3/1 = 3
The next 2 terms would be:
81 × 3 = 243
243 × 3 = 729
Hence the common ratio is 3 and the next 2 terms are 243 and 729.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...