Find the Batting Average of a batsman
Last Updated :
06 Dec, 2022
Given three integers runs, matches, and not-out representing the number of runs scored, number of innings played by the batsman and number of times he remained Not Out respectively, the task is to calculate the Batting Average of the batsman.
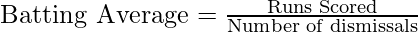
where
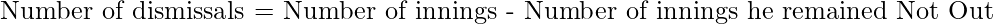
Note: If the batsman was never dismissed, print “NA” as the no average can be defined.
Examples:
Input: runs = 10000, matches = 250, not-out = 50
Output: 50
Explanation:
Number of times batsman was dismissed = 250 – 50 = 200
Batting Average = 10000 / 200 = 50.
Input: runs = 100, matches = 1, not-out = 1
Output: NA
Approach:
Follow the steps below to solve the problem:
- Calculate the number of dismissals, equal to matches – notout.
- Calculate the Batting Average, equal to runs/ (matches – notout).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double averageRuns(int runs,
int matches,
int notout)
{
int out = matches - notout;
if (out == 0)
return -1;
double avg = double(runs) / out;
return avg;
}
int main()
{
int runs = 10000;
int matches = 250;
int notout = 50;
double avg
= averageRuns(
runs, matches, notout);
if (avg == -1)
cout << "NA";
else
cout << avg;
return 0;
}
|
Java
import java.io.*;
public class GFG {
static int averageRuns(int runs, int matches,
int notout)
{
int out = matches - notout;
if (out == 0)
return -1;
int avg = (runs) / out;
return avg;
}
public static void main(String[] args)
{
int runs = 10000;
int matches = 250;
int notout = 50;
int avg = averageRuns(runs, matches, notout);
if (avg == -1)
System.out.print("NA");
else
System.out.print(avg);
}
}
|
Python3
def averageRuns(runs, matches, notout):
out = matches - notout;
if (out == 0):
return -1;
avg = runs // out;
return avg;
runs = 10000;
matches = 250;
notout = 50;
avg = averageRuns(runs, matches, notout);
if (avg == -1):
print("NA");
else:
print(avg);
|
C#
using System;
class GFG{
static int averageRuns(int runs,
int matches,
int notout)
{
int out1;
out1 = matches - notout;
if (out1 == 0)
return -1;
int avg = (runs) / out1;
return avg;
}
public static void Main (string[] args)
{
int runs = 10000;
int matches = 250;
int notout = 50;
int avg = averageRuns(runs, matches,
notout);
if (avg == -1)
Console.Write("NA");
else
Console.Write(avg);
}
}
|
Javascript
<script>
function averageRuns(runs, matches, notout)
{
let out1;
out1 = matches - notout;
if (out1 == 0)
return -1;
let avg = parseInt((runs) / out1, 10);
return avg;
}
let runs = 10000;
let matches = 250;
let notout = 50;
let avg = averageRuns(runs, matches, notout);
if (avg == -1)
document.write("NA");
else
document.write(avg);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...