Find the area of the rhombus whose side is 6 cm and altitude is 3.8 cm
Last Updated :
30 Jan, 2024
Rhombus is a kind of Quadrilateral, it is a 2-dimensional simple plane figure with a closed shape. A rhombus comes under the category of a parallelogram, and because of its unique properties, it gets a different identity as a quadrilateral. Rhombus has its all side are equal because of this property it is called an equilateral quadrilateral. Rhombus is derived from the Greek word ‘rhombus’, which literally means something that spins.
Rhombus
A rhombus is a kind is parallelogram as it follows the properties of a parallelogram, It has two pairs of parallel sides. Also, a rhombus also has four equal sides, but it is still a type of parallelogram with four congruent sides. Hence, a rhombus obeys all the properties of a parallelogram.
One should remember that Every rhombus is also a parallelogram, but not every parallelogram will be a rhombus. A square has also four equal sides, parallel and each side are perpendicular therefore we can say that square is a special case of a rhombus. All the angles of a square are right angles but in the case of the rhombus, it may or may not be right angles if a rhombus with right angles can be considered as a square. Hence, it can be concluded that:
- All rhombuses are parallelograms, but all parallelograms are not rhombuses.
- All rhombuses are not squares, but all squares are rhombuses.
A rhombus can also known by its three other names:
Properties of Rhombus
Basically, a rhombus is one of the types of a parallelogram, based on the characteristics of rhombus, the properties of a rhombus are:
- Opposite angles are congruent or equal.
- The opposite sides are equal and parallel.
- Diagonals bisect each other at a right angle.
- The Sum of any two adjacent angles is 180°.
Now consider the figure to understand the properties of Rhombus:

Figure of Rhombus
In Rhombus,
- All sides are equal i.e. AB = AC = CD = BD
- Diagonal bisect each other the angle of 90°. In the figure, ∠ 1 = ∠ 4= ∠ 2 = ∠ 3.
- Opposite sides are parallel and opposite angles are equal in rhombus, Here, CD ∥ AB and BD ∥ AC and ∠A = ∠D and ∠C = ∠B
The formula used in Rhombus,
If d1 and d2 are diagonals of the rhombus then,
Area of Rhombus = 1/2 × d1 × d2
OR
Area of Rhombus = Area of parallelogram = base × height
The perimeter of Rhombus = 4 × side.
Prove to the area of Rhombus:
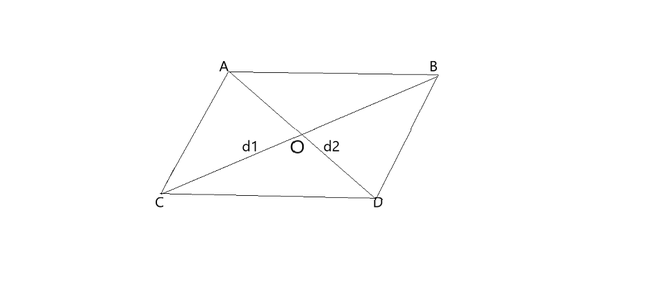
Consider a triangle ACD
Area of Triangle ACD = 1/2 × AD × d1/2 = 1/4 × CD × d1 — (Area of Triangle = 1/2 × base × height)
Now, consider, Area of Triangle ABD = 1/2 × AD × d2/2 = 1/4 × AB × d1
Area of Rhombus = Area of Triangle ACD + Area of Triangle ABD
= 1/4 × AD × d1 + 1/4 × AD × d1
= 1/4 × AD (d1 + d1)
= 1/4 × AD × 2d1
= 1/2(d1 × d2)
(AD = d1)
Hence, the area of the Rhombus is (d1 × d2)/2 square units.
Find the area of the rhombus whose side is 6 cm and altitude is 3.8 cm
Solution: side of rhombus = 6 cm
Altitude of rhombus = 3.8 cm
Area of Rhombus = base × height = 6 × 3.8
= 22.8 cm2
Sample question
Question 1: If the diagonals of a rhombus are 9cm and 8cm. Calculate its area.
Solution:
Area of Rhombus = (d1 × d2)/2
= (9 × 8)/2 = 72/2
= 36 cm2
Question 2: The area of rhombus given was 100 square units and its length of a diagonal 20 units. find the length of the other diagonal?
Solution:
Given:
Area of rhombus = 100 Sq. units,
Diagonal d1 = 20 units
= (d1 × d2)/2
100 = (20 ×d2)/ 2
d2 = 10 units
The length of the other diagonal = 10 units
Question 3: If the area of the Rhombus is 315cm2 and the altitude is 15cm. find its area.
Solution:
Area of rhombus = b × h
b × 15 = 315
b = 315/15 = 21 cm
Perimeter of rhombus = 4 × side
= 4 × 21 = 84cm
Question 4: show that, The sum of two adjacent angles in a Rhombus is 180°.
Solution:

ABCD is a Rhombus with four angles ∠ A, ∠ B, ∠ C, ∠ D
To prove: ∠ A + ∠ B = 180°
Proof: AB ∥ CD and AC is transversal
In the transversal, interior angles on the same side of a transversal are supplementary.
Therefore, ∠A + ∠C = 180°
Similarly, ∠B + ∠D = 180°, ∠C + ∠D = 180° and ∠A + ∠B = 180°.
Hence, sum of any two adjacent angles of a parallelogram = 180°.
Question 5: If the area and perimeter of a rhombus are 315cm2 and 180cm respectively. Calculate its altitude.
Solution:
Perimeter of rhombus = 180cm
4 × s = 180
s = 45cm
Area of rhombus = b × h
315 = 45 × h
h = 315/45
h = 7cm
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...