Find the area of a square with side 5x2y
Last Updated :
29 Oct, 2021
Mathematics is a subject with vast scope. It is divided into various branches as arithmetic, algebra, geometry, statistics, etc. Mathematics becomes part of education from the very beginning. Initially, students are introduced to basic mathematics and later to its various branches as the level is upgraded.
Algebra is also one of the branches of mathematics that are introduced at the elementary level. The study of algebra involves the simplification of known and unknown values by algebraic operations. The known values of the equations are represented by real numbers and the unknown values are expressed by letters.
What are algebraic expressions?
Algebraic expressions are the combination of variables, coefficient of variables, constants, exponent values, and algebraic operations like addition, subtraction, multiplication, and division. Each combination of coefficient, variable and constant is known as the term. And, on the basis of these number of terms algebraic expressions are divided into three types.
Types of Algebraic expressions
| Expressions | Terms | Example |
|---|
| Monomial expression | 1 | 2x3 |
| Binomial expression | 2 | 5y-3 |
| Polynomial expression | more than 2 | 2x2+4xy-4 |
Find the area of a square with a side of 5x2y.
Solution:
Length of one side of square = 5x2y
As we know all sides of a square are equal to each other.
= (5x2y)2
= 25x4y2
Hence, the area of the square is 25x4y2.
Sample Questions
Question 1. If the value of 5x-2y is equal to 7 and xy is equal to 2. What is the value of (5x+2y)2.
Solution:
Given,
5x-2y=7………..(I)
xy=2……………..(ii)
Squaring equation (I) on both sides ,
=>(5x-2y)2=(7)2
=>25x2+4y2-20xy=49
Substituting the value of equation (ii)
=>25x2+4y2=49+20xy
=>25x2+4y2=49+20×2
=>25x2+4y2=89…………..(iii)
Now, finding the value of (5x+2y)2
=>(5x+2y)2= (5x)2+(2y)2+2(5x)(2y)
= 25x2+4y2+20xy
= 89+20×2
=>(5x+2y)2 =129
Hence, the value of (5x+2y)2 is 129.
Question 2. Find the perimeter of a square with side 2x.
Solution:
length of one side of square(l) = 2x
perimeter of square (P) = 4l
= 4(2x)
= 8x
Hence, the perimeter of the square is 8x.
Question 3. If a rectangle has area x2+12xy-27y2 and length x+9y, find breadth of the rectangle.
Solution:
Length of rectangle(l) = x+9y
Area of rectangle (A)= x2+12xy-27y2
Now,
breadth = Area/ length
= 
= 
= 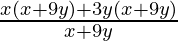
= 
= x+3y
Hence, the breadth of the rectangle is x+3y.
Question 4. Find the length of a rectangle having breadth x+3 and area of x2+7x+12.
Solution:
Area of rectangle(A) = x2+7x+12
Breadth (b) = x+3
Now,
Area = lengthX breadth
length = 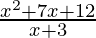
= 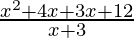
= 
= 
= x + 4
Hence, the length of the rectangle is x + 4.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...