Find the angle between tangents drawn from a given external point to a Circle

Last Updated : 19 Oct, 2022

Given a positive integer R representing the radius of the circle and the center of the circle (X1, Y1) and another point (X2, Y2) in the cartesian plane, the task is to find the angle between the pair of tangents drawn from the point (X2, Y2) to the circle.

Examples:

Input: R = 6, (X1, Y1) = (5, 1), (X2, Y2) = (6, 9)
Output: 96.1851

Input: R = 4, (X1, Y1) = (7, 12), (X2, Y2) = (3, 4)
Output: 53.1317

Approach: The given problem can be solved based on the following observations:

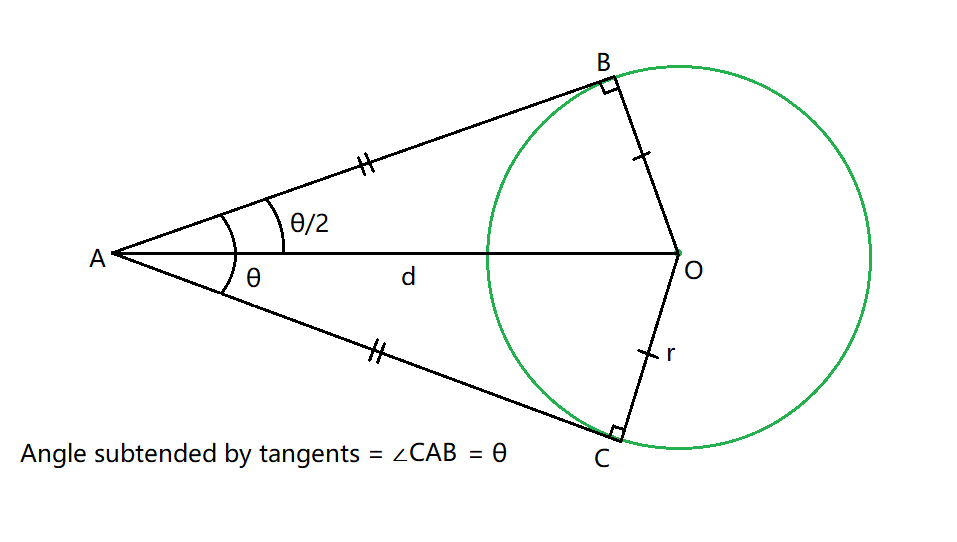
The radius makes an angle of 90 degrees with the tangent at the point of contact of the tangent and circle. Also, the angle subtended by the pair of tangents (?) is bisected by the line joining the center of the circle and the exterior point.
Therefore, the distance between the center and the exterior point can be calculated using the distance formula as:

Distance = 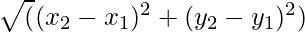$\sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)$

Now, consider d as the distance between the two given points, then In the right-angled triangle OAB,

=> $sin (\frac{\theta}{2}) = \frac{OB}{OA}$

=> $sin (\frac{\theta}{2}) = \frac{r}{d}$

=> $\frac{\theta}{2} = sin^{-1}(\frac{r}{d})$

=> $\theta = 2*sin^{-1}(\frac{r}{d})$

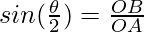
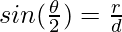
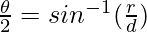
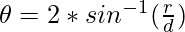
Therefore, using the above formula, the angle between the pair of tangents drawn from the point (X2, Y2) to the circle can be calculated.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
 
#include <cmath>
#include <iostream>
using namespace std;
 
// Function to find the distance between
// center and the exterior point
double point_distance(int x1, int y1,
                      int x2, int y2)
{
    // Find the difference between
    // the x and y coordinates
    int p = (x2 - x1);
    int q = (y2 - y1);
 
    // Using the distance formula
    double distance = sqrt(p * p
                           + q * q);
 
    return distance;
}
 
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
void tangentAngle(int x1, int y1,
                  int x2, int y2,
                  double radius)
{
    // Calculate the distance between
    // the center and exterior point
    double distance = point_distance(
        x1, y1, x2, y2);
 
    // Invalid Case
    if (radius / distance > 1
        || radius / distance < -1) {
        cout << -1;
    }
 
    // Find the angle using the formula
    double result
        = 2 * asin(radius / distance) * 180
          / 3.1415;
 
    // Print the resultant angle
    cout << result << " degrees";
}
 
// Driver Code
int main()
{
    int radius = 4;
    int x1 = 7, y1 = 12;
    int x2 = 3, y2 = 4;
    tangentAngle(x1, y1, x2, y2, radius);
 
    return 0;
}

Java

// java program for the above approach
import java.io.*;
import java.lang.*;
import java.util.*;
 
class GFG
{
   
// Function to find the distance between
// center and the exterior point
static double point_distance(int x1, int y1,
                      int x2, int y2)
{
    // Find the difference between
    // the x and y coordinates
    int p = (x2 - x1);
    int q = (y2 - y1);
  
    // Using the distance formula
    double distance = Math.sqrt(p * p
                           + q * q);
  
    return distance;
}
  
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
static void tangentAngle(int x1, int y1,
                  int x2, int y2,
                  double radius)
{
   
    // Calculate the distance between
    // the center and exterior point
    double distance = point_distance(
        x1, y1, x2, y2);
  
    // Invalid Case
    if (radius / distance > 1
        || radius / distance < -1) {
         System.out.println(-1);
    }
  
    // Find the angle using the formula
    double result
        = 2 * Math.asin(radius / distance) * 180
          / 3.1415;
  
    // Print the resultant angle
    System.out.println(String.format("%.4f", result) + " degrees");
}
   
    // Driver Code
    public static void main(String[] args)
    {
 
    int radius = 4;
    int x1 = 7, y1 = 12;
    int x2 = 3, y2 = 4;
    tangentAngle(x1, y1, x2, y2, radius);
    }
}
 
// This code is contributed by susmitakundugoaldanga.

Python3

# Python 3 program for the above approach
import math
 
# Function to find the distance between
# center and the exterior point
def point_distance(x1, y1,
                   x2,  y2):
 
    # Find the difference between
    # the x and y coordinates
    p = (x2 - x1)
    q = (y2 - y1)
 
    # Using the distance formula
    distance = math.sqrt(p * p
                         + q * q)
 
    return distance
 
# Function to find the angle between
# the pair of tangents drawn from the
# point (X2, Y2) to the circle.
def tangentAngle(x1,  y1,
                 x2,  y2,
                 radius):
 
    # Calculate the distance between
    # the center and exterior point
    distance = point_distance(
        x1, y1, x2, y2)
 
    # Invalid Case
    if (radius / distance > 1
            or radius / distance < -1):
        print(-1)
 
    # Find the angle using the formula
    result = 2 * math.asin(radius / distance) * 180 / 3.1415
 
    # Print the resultant angle
    print(result, " degrees")
 
# Driver Code
if __name__ == "__main__":
 
    radius = 4
    x1 = 7
    y1 = 12
    x2 = 3
    y2 = 4
    tangentAngle(x1, y1, x2, y2, radius)
 
    # This code is contributed by ukasp.

C#

// C# program for the above approach
using System;
 
class GFG{
 
// Function to find the distance between
// center and the exterior point
static double point_distance(int x1, int y1,
                             int x2, int y2)
{
     
    // Find the difference between
    // the x and y coordinates
    int p = (x2 - x1);
    int q = (y2 - y1);
 
    // Using the distance formula
    double distance = Math.Sqrt(p * p + q * q);
 
    return distance;
}
 
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
static void tangentAngle(int x1, int y1, int x2, 
                         int y2, double radius)
{
 
    // Calculate the distance between
    // the center and exterior point
    double distance = point_distance(x1, y1, x2, y2);
 
    // Invalid Case
    if (radius / distance > 1 || 
        radius / distance < -1)
    {
        Console.WriteLine(-1);
    }
 
    // Find the angle using the formula
    double result = 2 * Math.Asin(
               radius / distance) * 
                  180 / 3.1415;
 
    // Print the resultant angle
    Console.WriteLine(
        String.Format("{0:0.0000}", result) + 
                      " degrees");
}
 
// Driver code
static void Main()
{
    int radius = 4;
    int x1 = 7, y1 = 12;
    int x2 = 3, y2 = 4;
     
    tangentAngle(x1, y1, x2, y2, radius);
}
}
 
// This code is contributed by abhinavjain194

Javascript

<script>
 
// JavaScript program for the above approach
 
 
// Function to find the distance between
// center and the exterior point
function  point_distance( x1,  y1, x2,  y2)
{
     
    // Find the difference between
    // the x and y coordinates
    var p = (x2 - x1);
    var q = (y2 - y1);
 
    // Using the distance formula
    var distance = Math.sqrt(p * p + q * q);
 
    return distance;
}
 
// Function to find the angle between
// the pair of tangents drawn from the
// point (X2, Y2) to the circle.
 
function tangentAngle( x1,  y1,  x2, y2,  radius)
{
 
    // Calculate the distance between
    // the center and exterior point
    var distance = point_distance(x1, y1, x2, y2);
 
    // Invalid Case
    if (radius / distance > 1 || 
        radius / distance < -1)
    {
        document.write(-1 + "<br>");
    }
 
    // Find the angle using the formula
    var result = 2 * Math.asin(
               radius / distance) * 
                  180 / 3.1415;
 
    // Print the resultant angle
    document.write( result.toFixed(4) + " degrees");
     
}
 
// Driver code
 
    var radius = 4;
    var x1 = 7, y1 = 12;
    var x2 = 3, y2 = 4;
     
    tangentAngle(x1, y1, x2, y2, radius);
     
</script>