Sum of series M/1 + (M+P)/2 + (M+2*P)/4 + (M+3*P)/8……up to infinite

Find the sum of series M/1 + (M+P)/2 + (M+2*P)/4 + (M+3*P)/8……up to infinite where M and P are positive integers.

Examples: 

Input : M = 0, P = 3; 
Output : 6

Input : M = 2, P = 9;
Output : 22

Method : 
S = M/1 + (M + P)/2 + (M + 2*P)/4 + (M + 3*P) / 8……up to infinite
so the solution of this series will be like this
we are going to divide this series into two parts-
S = (M/1 + M/2 + M/4 + M/8……up to infinite) + ( p/2 + (2*p)/4 + (3*p)/8 + ….up to infinite) 
let us consider it
S = A + B ……..eq(1)
where, 
A = M/1 + M/2 + M/4 + M/8……up to infinite 
A = M*(1 + 1/2 + 1/4 + 1/8….up to infinite) 
which is G.P of infinite terms with r = 1/2;
According to the formula of G.P sum of infinite terms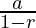for r < 1 and 
a is first term and r is common ratio so now, 
A = M * ( 1 / (1 – 1/2) ) 
A = 2 * M ; 

Now for B –
B = ( p/2 + (2*p)/4 + (3*p)/8 + ….up to infinite) 
B = P/2 * ( 1 + 2*(1/2) + 3*(1/4) + ……up to infinite)
it is sum of AGP of infinite terms with a = 1, r = 1/2 and d = 1;
According to the formula 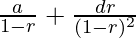where a is first term, 
r is common ratio and d is common difference so now,
B = P/2 * ( 1 / (1-1/2) + (1*1/2) / (1-1/2)^2 ) 
B = P/2 * 4 
B = 2*P ;
put value of A and B in eq(1) 
S = 2(M + P)

C++

#include <iostream>
using namespace std;

int sum(int M, int P)
{
    return 2*(M + P);
}

// driver code
int main() {

    int M = 2, P = 9;
    cout << sum(M,P);
    return 0;
}

Java

// Java Program to finding the
// sum of the series
import java.io.*;

class GFG {

    // function that calculate
    // the sum of the nth series
    static int sum_series(int M, int P)
    {
        return 2 * (M + P);
    }

    // Driver function
    public static void main (String[] args)
    {
        int M = 2;
        int P = 9;
        System.out.println( sum_series(M, P)) ;
    }
}

Python3

# Python3 Program to finding
# the sum of the  series

# function that calculate
# the sum of the  series
def sum_series(M, P):

    return int(2 * (M + P))

# Driver function
M = 2
P = 9
print(sum_series(M ,P))

C#

// C# program to finding the
// sum of the series
using System;

class GFG {

    // Function that calculate
    // the sum of the nth series
    static int sum_series(int M, int P)
    {
        return 2*(M + P);
    }

    // Driver Code
    public static void Main ()
    {
        int M =2;
        int P =9;

        Console.Write( sum_series(M,P)) ;
    }
}

PHP

<?php
// PHP program to finding the
// sum of the series

// Function that calculate
// the sum of the nth series
function sum($M, $P)
{
    return 2*($M + $P);
}

// Driver Code
$M = 2;
$P = 9;
echo sum($M, $P);

// This code is contributed by mits
?>

Javascript

<script>

// JavaScript program to finding the
// sum of the series

// Function that calculate
// the sum of the nth series
function sum_series(M, P)
{
    return 2 * (M + P);
}

// Driver code
let M = 2;
let P = 9;

document.write( sum_series(M, P));

// This code is contributed by splevel62

</script>

Output:

22

Time Complexity: O(1)

Auxiliary Space: O(1)