Find the sum of the series 1+11+111+1111+….. upto n terms
Last Updated :
25 May, 2022
Here we are going to find the sum of the series 1 + 11 + 111 + 1111 +…..upto N terms (where N is given).
Example :
Input : 3
Output : 1 + 11 + 111 +....
Total sum is : 123
Input : 4
Output : 1 + 11 + 111 + 1111 +.....
Total sum is : 1234
Input : 7
Output : 1 + 11 + 111 + 1111 + 11111 +
111111 + 1111111 +.....
Total sum is : 1234567
Here we see that when value of N is 3, series last upto 1 + 11 + 111 i.e, three term and it’s sum is 123.
Program for finding sum of above series :
C++
#include <bits/stdc++.h>
using namespace std;
int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++) {
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
int main()
{
int n = 5;
cout << " " << summation(n);
return 0;
}
|
C
#include <stdio.h>
int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++) {
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
int main()
{
int n = 5;
printf("%d", summation(n));
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++)
{
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
public static void main(String args[])
{
int n = 5;
System.out.println(summation(n));
}
}
|
Python
def summation(n):
sum = 0
j = 1
for i in range(1, n + 1):
sum = sum + j
j = (j * 10) + 1
return sum
n = 5
print(summation(n))
|
C#
using System;
class GFG
{
static int summation(int n)
{
int sum = 0, j = 1;
for (int i = 1; i <= n; i++)
{
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
public static void Main()
{
int n = 5;
Console.WriteLine(summation(n));
}
}
|
PHP
<?php
function summation($n)
{
$sum = 0; $j = 1;
for ($i = 1; $i <= $n; $i++)
{
$sum = $sum + $j;
$j = ($j * 10) + 1;
}
return $sum;
}
$n = 5;
echo summation($n);
?>
|
Javascript
<script>
function summation( n) {
let sum = 0, j = 1;
for ( let i = 1; i <= n; i++) {
sum = sum + j;
j = (j * 10) + 1;
}
return sum;
}
let n = 5;
document.write(summation(n));
</script>
|
Output :
12345
Time Complexity: O(n), where n represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Another method: Let given a series S = 1 + 11 + 111 + 1111 + . . . + upto nth term. Using formula to find sum of series.
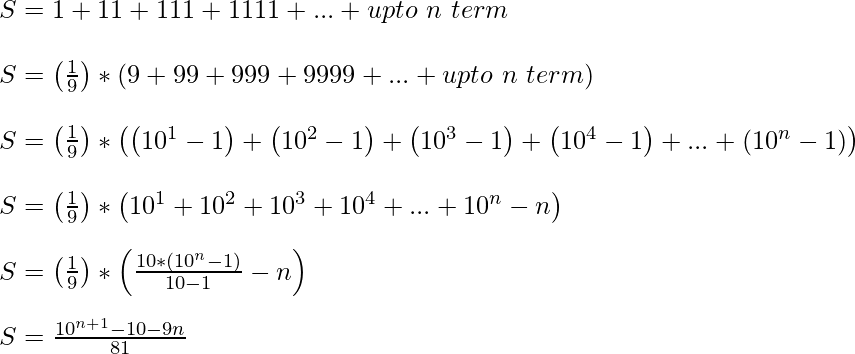
Below is the implementation of above approach.
C++
#include <bits/stdc++.h>
int summation(int n)
{
int sum;
sum = (pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
int main()
{
int n = 5;
printf("%d", summation(n));
return 0;
}
|
Java
import java.io.*;
class GFG {
static int summation(int n)
{
int sum;
sum = (int)(Math.pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
public static void main (String[] args)
{
int n = 5;
System.out.println(summation(n));
}
}
|
Python3
import math
def summation(n):
return int((pow(10, n + 1) -
10 - (9 * n)) / 81);
print(summation(5));
|
C#
using System;
class GFG {
static int summation(int n)
{
int sum;
sum = (int)(Math.Pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
public static void Main ()
{
int n = 5;
Console.WriteLine(summation(n));
}
}
|
PHP
<?php
function summation($n)
{
$sum;
$sum = (pow(10, $n + 1) -
10 - (9 * $n)) / 81;
return $sum;
}
$n = 5;
echo summation($n);
?>
|
Javascript
<script>
function summation( n)
{
let sum;
sum = (Math.pow(10, n + 1) -
10 - (9 * n)) / 81;
return sum;
}
let n = 5;
document.write(summation(n)) ;
</script>
|
Output :
12345
Time Complexity: O(logn), where n represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...