Find sum of product of number in given series
Last Updated :
30 Aug, 2022
Given two numbers N and T where,  and
and  . The task is to find the value of
. The task is to find the value of 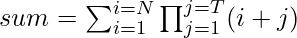 .
.
Since sum can be large, output it modulo 109+7.
Examples:
Input : 3 2
Output : 38
2*3 + 3*4 + 4*5 = 38
Input : 4 2
Output : 68
In the Given Sample Case n = 3 and t = 2.
sum = 2*3+3*4+4*5.
Notice that:


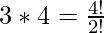
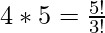
So each term is of the form 
If we multiply and divide by t! it becomes 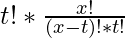
Which is nothing but 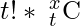
Therefore, 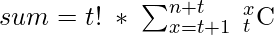
But we know 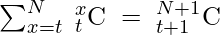
Therefore 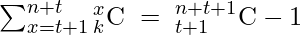
So final expression comes out to be 
But since n is so large we can not calculate it directly, we have to Simplify the above expression.
On Simplifying we get 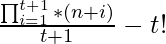 .
.
Below is the implementation of above approach
C++
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const long long MOD = 1000000007;
ll power(ll x, unsigned long long y, ll p)
{
ll res = 1;
x = x % p;
while (y > 0) {
if (y & 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
ll sumProd(ll n, ll t)
{
ll dino = power(t + 1, MOD - 2, MOD);
unsigned long long ans = 1;
for (ll i = n + t + 1; i > n; --i)
ans = (ans % MOD * i % MOD) % MOD;
ll tfact = 1;
for (int i = 1; i <= t; ++i)
tfact = (tfact * i) % MOD;
ans = ans * dino - tfact + MOD;
return ans % MOD;
}
int main()
{
ll n = 3, t = 2;
cout << sumProd(n, t);
return 0;
}
|
Java
public class GFG {
static long MOD = 1000000007;
static long power(long x, long y, long p)
{
long res = 1;
x = x % p;
while (y > 0) {
if ((y & 1)!= 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
static long sumProd(long n, long t)
{
long dino = power(t + 1, MOD - 2, MOD);
long ans = 1;
for (long i = n + t + 1; i > n; --i)
ans = (ans % MOD * i % MOD) % MOD;
long tfact = 1;
for (int i = 1; i <= t; ++i)
tfact = (tfact * i) % MOD;
ans = ans * dino - tfact + MOD;
return ans % MOD;
}
public static void main(String[] args) {
long n = 3, t = 2;
System.out.println(sumProd(n, t));
}
}
|
Python3
MOD = 1000000007
def power(x, y, p) :
res = 1
x = x % p
while y > 0 :
if y & 1 :
res = (res * x) % p
y = y >> 1
x = (x * x) % p
return res
def sumProd(n, t) :
dino = power(t + 1, MOD - 2, MOD)
ans = 1
for i in range(n + t + 1 , n, -1) :
ans = (ans % MOD * i % MOD) % MOD
tfact = 1
for i in range(1, t+1) :
tfact = (tfact * i) % MOD
ans = ans * dino - tfact + MOD
return ans % MOD
if __name__ == "__main__" :
n, t = 3, 2
print(sumProd(n, t))
|
C#
using System;
class GFG
{
static long MOD = 1000000007;
static long power(long x, long y,
long p)
{
long res = 1;
x = x % p;
while (y > 0)
{
if ((y & 1) != 0)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
static long sumProd(long n, long t)
{
long dino = power(t + 1, MOD - 2, MOD);
long ans = 1;
for (long i = n + t + 1; i > n; --i)
ans = (ans % MOD * i % MOD) % MOD;
long tfact = 1;
for (int i = 1; i <= t; ++i)
tfact = (tfact * i) % MOD;
ans = ans * dino - tfact + MOD;
return ans % MOD;
}
public static void Main()
{
long n = 3, t = 2;
Console.WriteLine(sumProd(n, t));
}
}
|
PHP
<?php
function power($x, $y, $p)
{
$res = 1;
$x = $x % $p;
while ($y > 0)
{
if ($y & 1)
$res = ($res * $x) % $p;
$y = $y >> 1;
$x = ($x * $x) % $p;
}
return $res;
}
function sumProd($n, $t)
{
$MOD = 1000000007;
$dino = power($t + 1, $MOD - 2, $MOD);
$ans = 1;
for ($i = $n + $t + 1; $i > $n; --$i)
$ans = ($ans % $MOD * $i %
$MOD) % $MOD;
$tfact = 1;
for ($i = 1; $i <= $t; ++$i)
$tfact = ($tfact * $i) % $MOD;
$ans = $ans * $dino - $tfact + $MOD;
return $ans % $MOD;
}
$n = 3;
$t = 2;
echo sumProd($n, $t);
?>
|
Javascript
<script>
var MOD = 100000007;
function power(x, y, p)
{
var res = 1;
x = x % p;
while (y > 0) {
if (y & 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
function sumProd(n, t)
{
var dino = power(t + 1, MOD - 2, MOD);
var ans = 1;
for (var i = n + t + 1; i > n; --i)
ans = (ans % MOD * i % MOD) % MOD;
var tfact = 1;
for (var i = 1; i <= t; ++i)
tfact = (tfact * i) % MOD;
ans = ans * dino - tfact + MOD;
return ans % MOD;
}
var n = 3, t = 2;
document.write( sumProd(n, t));
</script>
|
Output:
38
Time Complexity: O(n+t)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...